0.5 Is What Percent Of 20
listenit
May 23, 2025 · 4 min read
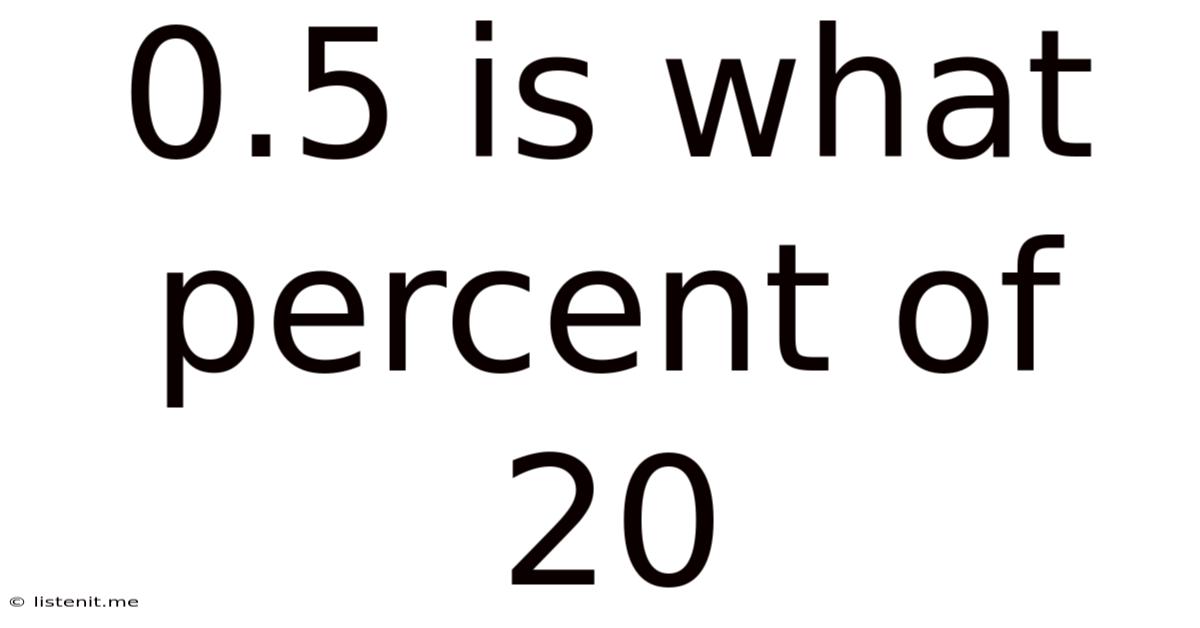
Table of Contents
0.5 is What Percent of 20? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will delve into the seemingly simple question, "0.5 is what percent of 20?", and explore the underlying concepts and methods involved in solving percentage problems. We'll go beyond just finding the answer and examine different approaches, practical applications, and even touch upon advanced percentage calculations.
Understanding the Basics of Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Key Components of Percentage Problems:
- Part: The value that represents a portion of the whole. In our problem, 0.5 is the part.
- Whole: The total value or the complete amount. In our problem, 20 is the whole.
- Percentage: The ratio of the part to the whole, expressed as a number out of 100. This is what we need to find.
Calculating "0.5 is What Percent of 20?"
There are several ways to solve this percentage problem. Let's explore the most common methods:
Method 1: Using the Formula
The basic percentage formula is:
(Part / Whole) x 100 = Percentage
Substituting the values from our problem:
(0.5 / 20) x 100 = Percentage
0.025 x 100 = 2.5%
Therefore, 0.5 is 2.5% of 20.
Method 2: Using Proportions
We can set up a proportion to solve the problem:
0.5 / 20 = x / 100
Cross-multiplying, we get:
20x = 500
Dividing both sides by 20:
x = 25
Therefore, x represents 2.5%, confirming our previous result. This method highlights the relationship between fractions and percentages.
Method 3: Thinking in Decimals
Since percentages are essentially fractions with a denominator of 100, we can directly convert the fraction 0.5/20 to a decimal and then multiply by 100:
0.5 divided by 20 = 0.025
0.025 x 100 = 2.5%
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world situations:
1. Financial Calculations:
- Interest Rates: Calculating simple and compound interest on loans, investments, and savings accounts. Understanding percentage changes in interest rates is also essential.
- Discounts and Sales Tax: Determining the final price of an item after applying discounts or adding sales tax.
- Profit and Loss: Calculating the profit or loss percentage on a business transaction.
- Investment Returns: Analyzing the returns on investments, considering factors like dividends and capital appreciation.
2. Data Analysis and Statistics:
- Statistical Representation: Percentages are frequently used to represent data in graphs, charts, and reports to show proportions and trends.
- Probability and Risk Assessment: Expressing probabilities and risks as percentages helps in making informed decisions.
- Market Research: Analyzing market share, customer satisfaction, and other key metrics using percentages.
3. Everyday Life:
- Tip Calculation: Calculating appropriate tips in restaurants.
- Grading and Scores: Interpreting grades and scores expressed as percentages.
- Recipe Scaling: Adjusting recipe ingredients based on percentage changes in serving sizes.
Advanced Percentage Calculations
While our initial problem was relatively straightforward, let's explore more complex scenarios:
1. Percentage Increase and Decrease:
Calculating the percentage increase or decrease between two values requires a slightly different approach. The formula for percentage change is:
[(New Value - Old Value) / Old Value] x 100 = Percentage Change
For example, if a value increases from 20 to 25, the percentage increase is:
[(25 - 20) / 20] x 100 = 25%
2. Finding the Original Value:
If you know the percentage and the final value after a percentage increase or decrease, you can work backward to find the original value. This often involves using algebraic equations.
3. Compound Percentage Changes:
When dealing with successive percentage changes, it's important to understand that they don't simply add up. Compounding effects need to be considered. This is crucial in finance, where compound interest significantly impacts long-term investment growth.
Tips and Tricks for Mastering Percentages
- Practice Regularly: The more you practice solving percentage problems, the more comfortable and efficient you'll become.
- Understand the Concepts: Focus on grasping the underlying principles rather than just memorizing formulas.
- Use Different Methods: Try solving problems using different approaches to reinforce your understanding and identify the most efficient method for you.
- Use Calculators Wisely: While calculators can be helpful, don't rely on them entirely. Develop your mental math skills to quickly estimate percentages.
- Check Your Work: Always double-check your calculations to avoid errors.
Conclusion: More Than Just a Simple Calculation
The seemingly simple question, "0.5 is what percent of 20?", serves as a gateway to a broader understanding of percentage calculations and their widespread applications. From basic arithmetic to complex financial modeling, mastering percentages is a valuable skill that enhances problem-solving abilities and facilitates informed decision-making across various fields. By understanding the underlying concepts and applying different solution methods, you can confidently tackle diverse percentage-related problems and apply this knowledge to real-world situations. Remember to practice regularly and explore more advanced percentage calculations to further enhance your skills.
Latest Posts
Latest Posts
-
How Much Is 55 000 A Year After Taxes
May 24, 2025
-
What Is 20 Off Of 60 Dollars
May 24, 2025
-
The Number 18 Is Which Percent Of 15
May 24, 2025
-
12 Out Of 30 Is What Percent
May 24, 2025
-
5 To The Power Of 12
May 24, 2025
Related Post
Thank you for visiting our website which covers about 0.5 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.