12 Out Of 50 As A Percentage
listenit
May 25, 2025 · 5 min read
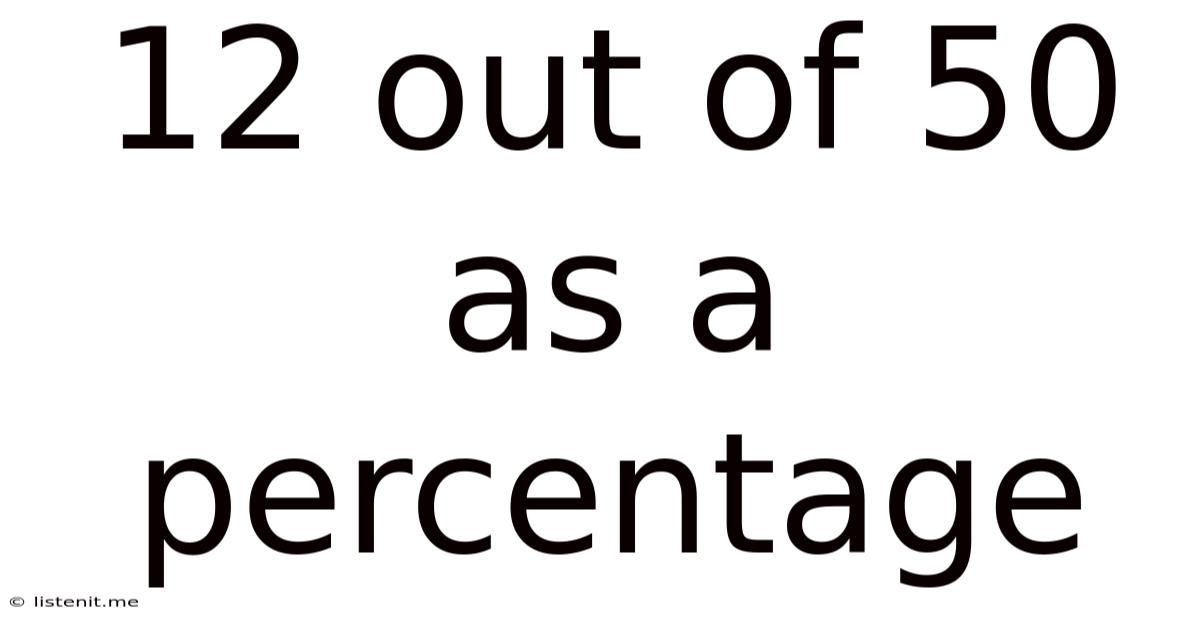
Table of Contents
12 out of 50 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill in various aspects of life, from everyday budgeting to complex statistical analysis. Understanding how to convert fractions to percentages is crucial for making informed decisions and interpreting data effectively. This comprehensive guide will delve deep into calculating "12 out of 50 as a percentage," exploring the process, its applications, and related concepts. We'll also examine different methods to achieve the same result, ensuring you gain a solid understanding of this essential mathematical operation.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is simply a fraction or ratio expressed as a number out of 100. The term "percent" itself comes from the Latin "per centum," meaning "out of one hundred." This means that 25%, for instance, represents 25 parts out of 100 equal parts.
Method 1: Using the Basic Percentage Formula
The most straightforward method to calculate "12 out of 50 as a percentage" involves using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 12 (the number we're considering as a portion of the whole)
- Whole: 50 (the total number)
Substituting these values into the formula:
(12 / 50) * 100% = 24%
Therefore, 12 out of 50 is 24%.
Method 2: Simplifying the Fraction First
We can simplify the fraction 12/50 before applying the percentage formula. Both the numerator (12) and the denominator (50) are divisible by 2:
12 / 50 = 6 / 25
Now, we can apply the percentage formula:
(6 / 25) * 100% = 24%
This method demonstrates that simplifying the fraction beforehand can sometimes make the calculation easier.
Method 3: Using Decimal Conversion
Another approach involves converting the fraction to a decimal first, then multiplying by 100%:
12 / 50 = 0.24
0.24 * 100% = 24%
This method highlights the close relationship between decimals and percentages. A decimal can be easily converted to a percentage by multiplying by 100.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages has numerous practical applications across various fields:
1. Finance and Budgeting:
- Interest rates: Calculating simple and compound interest on loans and investments.
- Discounts and sales: Determining the final price of an item after a percentage discount.
- Tax calculations: Computing the amount of tax payable on income or purchases.
- Investment returns: Measuring the performance of investments in terms of percentage growth or loss.
2. Academic Performance:
- Grade calculations: Determining final grades based on weighted percentages of assignments and exams.
- Test scores: Expressing the number of correct answers as a percentage of the total questions.
- Performance metrics: Evaluating student progress and identifying areas needing improvement.
3. Data Analysis and Statistics:
- Proportions and ratios: Representing data as percentages to facilitate comparison and interpretation.
- Surveys and polls: Presenting survey results and public opinion in percentage terms.
- Probability and chance: Expressing the likelihood of events occurring as percentages.
4. Business and Marketing:
- Market share: Analyzing the percentage of a market held by a particular company or product.
- Sales growth: Tracking the percentage increase or decrease in sales over time.
- Conversion rates: Measuring the percentage of website visitors who complete a desired action (e.g., making a purchase).
- Customer satisfaction: Assessing customer satisfaction levels using percentage scores.
5. Everyday Life:
- Tipping in restaurants: Calculating the appropriate tip percentage based on the bill amount.
- Recipe scaling: Adjusting ingredient quantities in recipes based on percentage increases or decreases.
- Sales tax: Calculating sales tax based on a percentage of the purchase price.
Beyond the Basic Calculation: Understanding Percentage Change
While calculating "12 out of 50 as a percentage" focuses on a static proportion, understanding percentage change is equally important in many real-world scenarios. Percentage change calculates the proportional difference between an initial value and a final value.
The formula for percentage change is:
[(New Value - Old Value) / Old Value] * 100% = Percentage Change
For example, if a stock price increases from $50 to $60, the percentage change would be:
[(60 - 50) / 50] * 100% = 20%
This indicates a 20% increase in the stock price. Similarly, a decrease would result in a negative percentage change.
Advanced Applications and Considerations
The principles of calculating percentages extend to more complex scenarios:
- Weighted averages: Calculating averages where different values contribute different weights or percentages to the overall result.
- Compound interest: Calculating interest where the interest earned in each period is added to the principal amount before calculating the next period's interest. This leads to exponential growth over time.
- Statistical analysis: Percentages play a vital role in statistical analysis, helping researchers to summarize and interpret data. Hypothesis testing and confidence intervals often involve percentage calculations.
Practical Tips for Accurate Percentage Calculations
- Double-check your work: Always verify your calculations to avoid errors. Using a calculator can minimize the risk of human error.
- Understand the context: Pay attention to the meaning of the numbers involved. Understanding what the "part" and "whole" represent in a problem is crucial for accurate calculation.
- Use appropriate tools: Calculators, spreadsheets, and specialized software can greatly assist in percentage calculations, especially for more complex problems.
- Practice regularly: The more you practice calculating percentages, the more proficient you'll become.
Conclusion: Mastering Percentage Calculations
Calculating "12 out of 50 as a percentage," while seemingly simple, serves as a gateway to understanding a broad range of percentage-based calculations. By mastering the basic formula and understanding its various applications, you equip yourself with a valuable tool for tackling numerous challenges in finance, academics, data analysis, business, and daily life. Remember the different approaches presented – using the basic formula, simplifying the fraction, or employing decimal conversion – and choose the method best suited for the context. Consistent practice and attention to detail will significantly improve your proficiency in this crucial mathematical skill.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 4xy2 And 20x2y4
May 25, 2025
-
12 Weeks From October 1 2024
May 25, 2025
-
72000 A Year Is How Much A Month
May 25, 2025
-
What Time Would It Be 9 Hours From Now
May 25, 2025
-
4 Is What Percent Of 19
May 25, 2025
Related Post
Thank you for visiting our website which covers about 12 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.