What Is The Greatest Common Factor Of 4xy2 And 20x2y4
listenit
May 25, 2025 · 5 min read
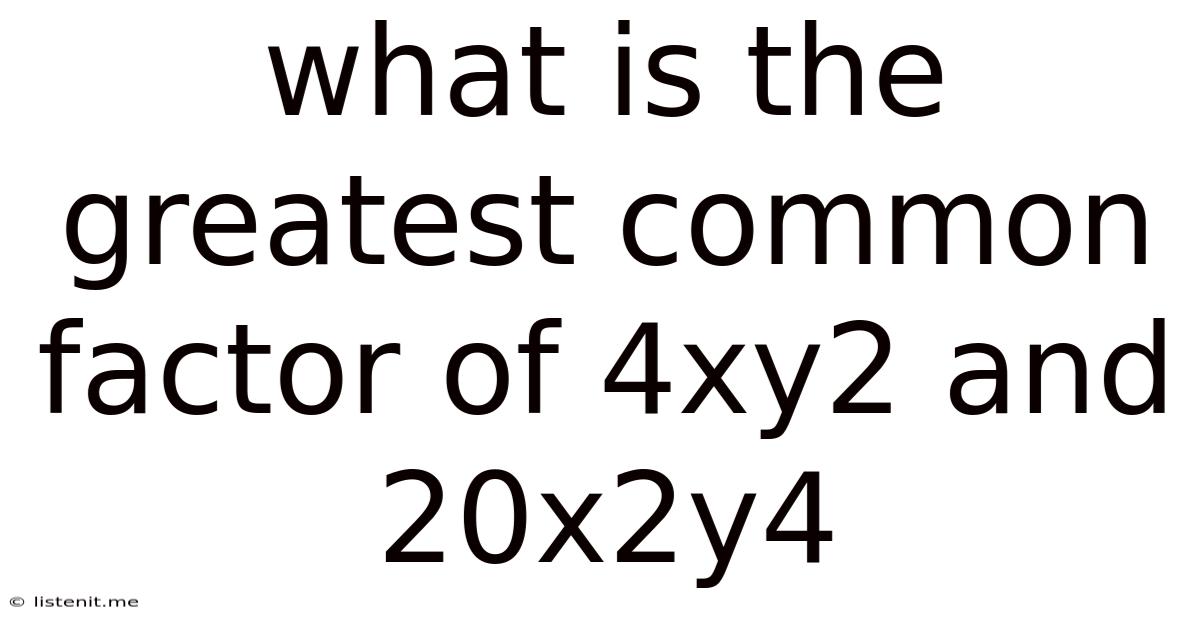
Table of Contents
What is the Greatest Common Factor of 4xy² and 20x²y⁴? A Deep Dive into Finding GCFs
Finding the greatest common factor (GCF) is a fundamental concept in mathematics, particularly crucial in algebra and number theory. Understanding how to determine the GCF allows for simplification of expressions, factoring polynomials, and solving various mathematical problems. This article will delve into the process of finding the GCF, specifically focusing on the example of 4xy² and 20x²y⁴, and expand on the broader applications of this concept.
Understanding Greatest Common Factors (GCFs)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides evenly into two or more numbers without leaving a remainder. For variables with exponents, it represents the highest power of each variable that divides both terms. The GCF is a crucial tool for simplifying algebraic expressions and solving equations.
Finding the GCF of Numbers
Before tackling variables, let's review finding the GCF of numbers. Consider the numbers 12 and 18. We can list their factors:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
The common factors are 1, 2, 3, and 6. The greatest of these is 6, therefore, the GCF(12, 18) = 6.
Alternatively, we can use prime factorization. Breaking down each number into its prime factors:
- 12 = 2² x 3
- 18 = 2 x 3²
The GCF is found by taking the lowest power of each common prime factor. In this case, we have one 2 and one 3, resulting in a GCF of 2 x 3 = 6.
Finding the GCF of Algebraic Expressions: 4xy² and 20x²y⁴
Now, let's apply this knowledge to the algebraic expressions 4xy² and 20x²y⁴. We'll break down the process step-by-step:
1. Find the GCF of the Coefficients
First, consider the numerical coefficients: 4 and 20. Using prime factorization:
- 4 = 2²
- 20 = 2² x 5
The lowest power of the common prime factor 2 is 2². Therefore, the GCF of the coefficients is 2² = 4.
2. Find the GCF of the Variables
Next, examine the variables x and y. Remember that the GCF of variables involves selecting the lowest power of each common variable:
- Variable x: The lowest power of x is x¹ (present in 4xy²).
- Variable y: The lowest power of y is y² (present in 4xy²).
Therefore, the GCF of the variables is xy².
3. Combine the GCFs
Finally, combine the GCF of the coefficients and the GCF of the variables to obtain the overall GCF of the expressions:
GCF(4xy², 20x²y⁴) = 4xy²
Applications of Finding the Greatest Common Factor
The ability to find the greatest common factor has far-reaching applications in various mathematical contexts:
1. Simplifying Algebraic Expressions
Finding the GCF is essential for simplifying algebraic expressions. By factoring out the GCF, we can reduce expressions to their simplest forms, making them easier to work with. For instance:
12x³ + 18x² = 6x²(2x + 3) (Here, 6x² is the GCF)
This simplified form is much more manageable for further algebraic operations.
2. Factoring Polynomials
The GCF plays a critical role in factoring polynomials, a crucial step in solving polynomial equations. Consider the polynomial:
4x²y + 8xy² - 12xy
The GCF of the terms is 4xy. Factoring this out:
4xy(x + 2y - 3)
This factored form is invaluable for finding the roots (solutions) of the polynomial equation 4x²y + 8xy² - 12xy = 0.
3. Solving Equations
The GCF helps in simplifying and solving various types of equations. For example, consider the equation:
6x²y - 12xy² = 0
Factoring out the GCF, 6xy, we get:
6xy(x - 2y) = 0
This leads to two potential solutions: x = 0 or x = 2y.
4. Fraction Simplification
The GCF is used extensively in simplifying fractions, both numerical and algebraic. When both the numerator and the denominator of a fraction share a common factor, we can divide both by the GCF to obtain a simplified fraction. For example:
12/18 = (6 x 2)/(6 x 3) = 2/3 (Here, 6 is the GCF)
5. Least Common Multiple (LCM) Calculation
While seemingly different, the GCF and the Least Common Multiple (LCM) are closely related. The LCM is the smallest number that is a multiple of both numbers. There's a useful relationship between the GCF and LCM:
LCM(a, b) = (a x b) / GCF(a, b)
Knowing the GCF allows for a quick calculation of the LCM, vital in operations involving fractions and algebraic expressions.
Advanced Techniques for Finding GCFs
For more complex expressions or larger sets of numbers, more sophisticated techniques are available:
Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers. It involves repeated division until the remainder is 0. The last non-zero remainder is the GCF.
Prime Factorization Method (for larger numbers)
For larger numbers, prime factorization becomes more efficient. Finding the prime factors of each number and identifying the common factors with the lowest powers remains the most reliable method.
GCF of Polynomials with Multiple Variables
Extending the concept to polynomials with multiple variables involves systematically finding the lowest power of each common variable and combining it with the GCF of the coefficients. The principles remain the same; the complexity simply increases with the number of variables and their exponents.
Conclusion: The Importance of Mastering GCFs
Understanding and efficiently calculating the greatest common factor is crucial for success in algebra and beyond. Its applications extend far beyond simple number simplification, playing a critical role in simplifying expressions, factoring polynomials, solving equations, and even performing calculations related to the least common multiple. Mastering this fundamental mathematical concept will undoubtedly strengthen your problem-solving skills across various mathematical disciplines. By understanding the underlying principles and employing appropriate techniques, finding the GCF becomes a straightforward and powerful tool in your mathematical toolkit.
Latest Posts
Latest Posts
-
1 Out Of 22 As A Percentage
May 25, 2025
-
Buy New Or Used Car Calculator
May 25, 2025
-
What Is 1 4 Of 36
May 25, 2025
-
What Percent Of 77 5 Is 28 52
May 25, 2025
-
How Old Is Someone Born In 87
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 4xy2 And 20x2y4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.