1/12 Of 1/3 Is What Fraction
listenit
May 25, 2025 · 5 min read
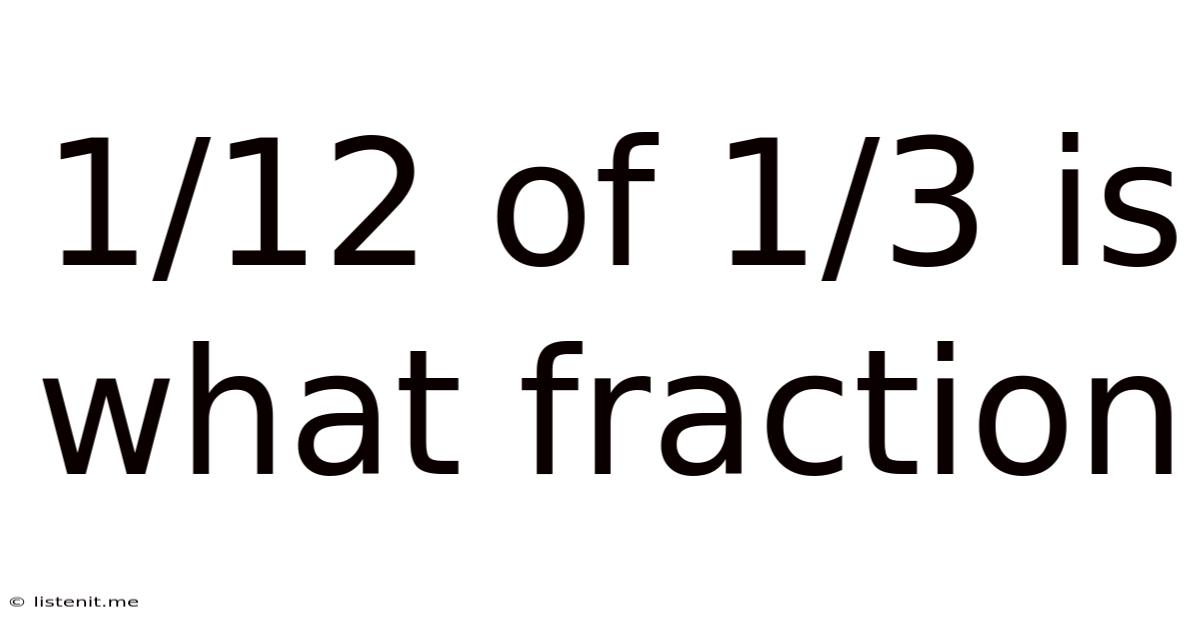
Table of Contents
1/12 of 1/3 is What Fraction? A Deep Dive into Fraction Multiplication
This seemingly simple question, "1/12 of 1/3 is what fraction?", opens the door to a deeper understanding of fraction multiplication, a fundamental concept in mathematics with wide-ranging applications. This comprehensive guide will not only answer the question but also explore the underlying principles, provide practical examples, and offer strategies to confidently tackle similar problems. We'll even delve into the real-world applications of fraction multiplication.
Understanding the Fundamentals: Fractions and Multiplication
Before we tackle the specific problem, let's solidify our understanding of fractions and how they are multiplied. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
Key Concept: The word "of" in mathematics, especially when dealing with fractions, signifies multiplication. So, "1/12 of 1/3" translates directly to (1/12) x (1/3).
Solving the Problem: 1/12 of 1/3
To multiply fractions, we follow these simple steps:
- Multiply the numerators: Multiply the top numbers together. In our case, 1 x 1 = 1.
- Multiply the denominators: Multiply the bottom numbers together. In our case, 12 x 3 = 36.
- Simplify the resulting fraction: The resulting fraction is 1/36. In this instance, the fraction is already in its simplest form because the greatest common divisor (GCD) of 1 and 36 is 1. There are no common factors to cancel out.
Therefore, the answer to the question "1/12 of 1/3 is what fraction?" is 1/36.
Visualizing Fraction Multiplication
Visual aids can greatly enhance our understanding of fraction multiplication. Imagine a rectangular pizza.
-
1/3 of the pizza: Divide the pizza into three equal slices. 1/3 represents one of these slices.
-
1/12 of 1/3: Now, take that 1/3 slice and divide it into twelve equal parts. 1/12 of the 1/3 slice represents one of these smaller parts.
To find the fraction representing this tiny piece relative to the whole pizza, we would need to divide the entire pizza into 36 equal pieces (3 x 12). Our small piece is only one of these 36 pieces, hence 1/36.
More Examples of Fraction Multiplication
Let's reinforce our understanding with a few more examples:
Example 1:
What is 2/5 of 3/4?
- Multiply numerators: 2 x 3 = 6
- Multiply denominators: 5 x 4 = 20
- Simplify: 6/20 simplifies to 3/10 (dividing both numerator and denominator by 2)
Therefore, 2/5 of 3/4 is 3/10.
Example 2:
What is 1/4 of 2/3?
- Multiply numerators: 1 x 2 = 2
- Multiply denominators: 4 x 3 = 12
- Simplify: 2/12 simplifies to 1/6 (dividing both numerator and denominator by 2)
Therefore, 1/4 of 2/3 is 1/6.
Example 3: (Involving Mixed Numbers)
What is 1 1/2 of 2/3?
First, convert the mixed number 1 1/2 into an improper fraction: (1 x 2) + 1 = 3/2
- Multiply numerators: 3 x 2 = 6
- Multiply denominators: 2 x 3 = 6
- Simplify: 6/6 simplifies to 1
Therefore, 1 1/2 of 2/3 is 1.
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't just a classroom exercise; it has numerous real-world applications:
-
Cooking and Baking: Scaling recipes up or down often involves multiplying fractions. For instance, if a recipe calls for 1/2 cup of flour and you want to make half the recipe, you'll need to calculate 1/2 of 1/2.
-
Construction and Engineering: Accurate measurements in construction and engineering projects frequently require working with fractions. Calculating the amount of materials needed often involves fraction multiplication.
-
Finance and Budgeting: Dealing with percentages, discounts, and interest calculations frequently involves fraction multiplication. For example, calculating a 15% discount on an item involves multiplying the original price by 15/100 (or 0.15).
-
Data Analysis: In data analysis and statistics, fractions and their multiplication are crucial for calculating proportions, probabilities, and various statistical measures.
Tips and Tricks for Mastering Fraction Multiplication
-
Practice Regularly: Consistent practice is key to mastering any mathematical concept. Work through numerous problems of varying complexity.
-
Visualize: Use visual aids like diagrams or real-world objects to help you understand the concept.
-
Simplify Early: Simplifying fractions before multiplication can often make calculations easier. Look for common factors in the numerators and denominators that can be cancelled out.
-
Check Your Answers: Always double-check your answers to ensure accuracy.
Conclusion: Beyond the Basics of 1/12 of 1/3
The seemingly simple question of "1/12 of 1/3" has served as a springboard to explore the broader world of fraction multiplication. Understanding this fundamental concept unlocks the ability to solve a wide range of mathematical problems and tackle real-world challenges involving fractions. By mastering the techniques outlined in this guide, you'll gain confidence in your ability to work with fractions and appreciate their widespread applications. Remember that consistent practice and a visual understanding are crucial for achieving mastery in this area. So, grab your pencil and paper, and keep practicing! You'll be amazed at how quickly your skills improve.
Latest Posts
Latest Posts
-
30 Is 12 Percent Of What Number
May 25, 2025
-
What Is The Greatest Common Factor Of 51 And 85
May 25, 2025
-
5 X 1 2 As A Fraction
May 25, 2025
-
Gcf Of 42 70 And 84
May 25, 2025
-
What Is The Greatest Common Factor Of 30 And 40
May 25, 2025
Related Post
Thank you for visiting our website which covers about 1/12 Of 1/3 Is What Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.