5 X 1/2 As A Fraction
listenit
May 25, 2025 · 5 min read
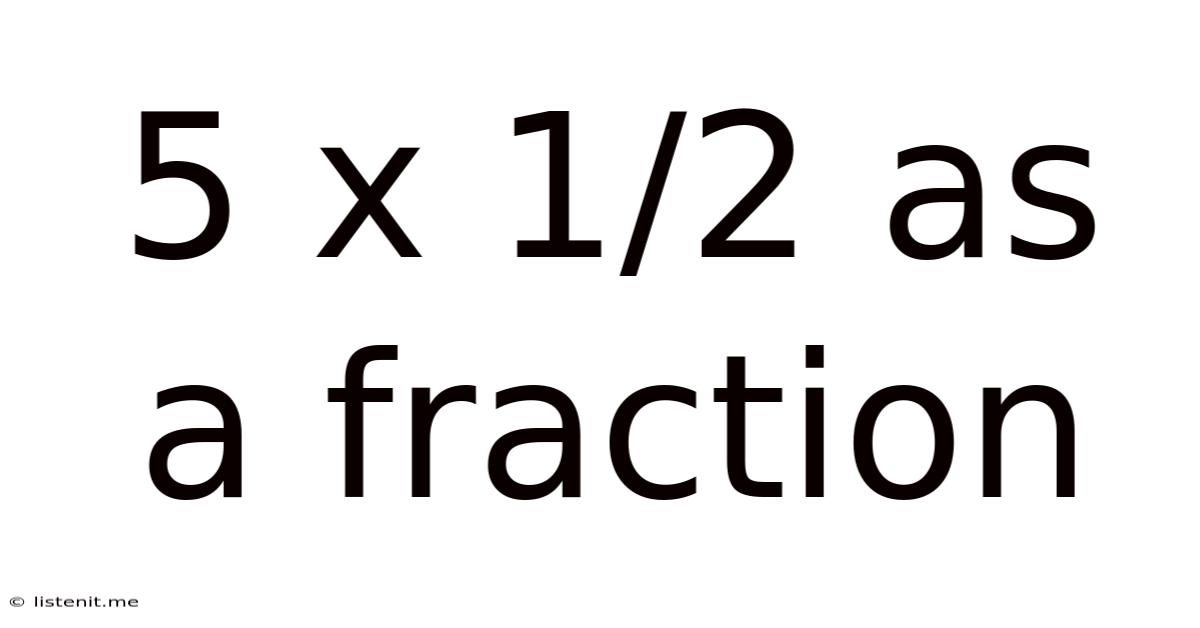
Table of Contents
5 x 1/2 as a Fraction: A Comprehensive Guide
Understanding fractions and how to manipulate them is a fundamental skill in mathematics. This comprehensive guide will delve into the seemingly simple problem of calculating 5 x 1/2 as a fraction, exploring various approaches, underlying concepts, and practical applications. We'll go beyond the basic calculation and delve into the broader mathematical principles at play, ensuring a thorough understanding for all readers, regardless of their current mathematical proficiency.
What Does 5 x 1/2 Mean?
Before we jump into the calculation, let's break down the meaning of the expression "5 x 1/2." This expression represents the multiplication of a whole number (5) by a fraction (1/2). In simpler terms, we're essentially finding out what five halves add up to. Think of it as having five pieces, each representing half of a whole.
Method 1: Direct Multiplication
The most straightforward approach is to perform the multiplication directly:
5 x 1/2 = (5 x 1) / 2 = 5/2
This simplifies to an improper fraction: 5/2. An improper fraction has a numerator (top number) larger than its denominator (bottom number). This is perfectly acceptable, and often preferred in mathematical calculations.
Method 2: Visual Representation
A visual representation can greatly aid in understanding. Imagine a whole divided into two equal halves. "1/2" represents one of these halves. If we have five of these halves (5 x 1/2), we have a total of five halves. We can visualize this as five half-circles arranged together, visually demonstrating that we have 5/2 or 2 1/2 wholes.
Method 3: Converting to a Mixed Number
While 5/2 is a perfectly valid answer, it's often beneficial to express it as a mixed number. A mixed number combines a whole number and a proper fraction (where the numerator is smaller than the denominator). To convert 5/2 to a mixed number, we perform a division:
5 ÷ 2 = 2 with a remainder of 1
This means that 5/2 is equivalent to 2 wholes and 1/2. Therefore, 5 x 1/2 = 2 1/2. This representation can be more intuitive and easier to grasp in certain contexts.
Understanding Fractions: A Deeper Dive
To fully grasp the calculation of 5 x 1/2, it's crucial to understand the core concepts related to fractions.
Numerator and Denominator:
The top number in a fraction is the numerator, indicating the number of parts we have. The bottom number is the denominator, indicating the total number of equal parts the whole is divided into.
Proper and Improper Fractions:
A proper fraction has a numerator smaller than the denominator (e.g., 1/2, 3/4). An improper fraction has a numerator greater than or equal to the denominator (e.g., 5/2, 7/3).
Mixed Numbers:
A mixed number combines a whole number and a proper fraction (e.g., 2 1/2, 3 2/3). These are useful for representing quantities that are greater than one.
Practical Applications
The ability to multiply fractions, as demonstrated by 5 x 1/2, has many practical applications in daily life and various fields.
-
Cooking and Baking: Recipes frequently require fractional amounts of ingredients. Calculating the correct quantities when scaling a recipe up or down relies heavily on understanding fraction multiplication. For example, if a recipe calls for 1/2 cup of flour and you want to make five times the recipe, you'll need 5 x 1/2 = 2 1/2 cups of flour.
-
Measurement and Construction: In carpentry, construction, and engineering, precise measurements are critical. Often these measurements involve fractions of inches or centimeters. Calculating areas, volumes, or material needs necessitates multiplying fractions.
-
Finance and Budgeting: Fractional values are commonly used in financial calculations, such as interest rates, stock prices, and calculating portions of a budget. Understanding fraction multiplication is essential for accurate financial management.
-
Data Analysis and Statistics: Fractions are frequently encountered in data analysis and statistics. Calculations involving proportions, probabilities, and data representation often involve multiplying and manipulating fractions.
-
Everyday Scenarios: From dividing a pizza amongst friends to calculating the portion of a task completed, fractions permeate everyday life. The ability to confidently work with fractions, including multiplication, makes navigating these situations much easier.
Further Exploration: Multiplying Fractions by Whole Numbers
The example of 5 x 1/2 demonstrates a specific instance of multiplying a whole number by a fraction. This concept can be generalized to any whole number and any fraction:
To multiply a whole number by a fraction, multiply the whole number by the numerator of the fraction and keep the same denominator.
For instance:
- 3 x 2/5 = (3 x 2) / 5 = 6/5
- 7 x 3/4 = (7 x 3) / 4 = 21/4
Remember, the resulting fraction can then be simplified or converted to a mixed number if needed.
Advanced Concepts: Multiplying Fractions by Fractions
Building upon the knowledge of multiplying whole numbers by fractions, let's explore the more general case of multiplying two fractions together.
To multiply two fractions:
- Multiply the numerators together.
- Multiply the denominators together.
- Simplify the resulting fraction if possible.
For example:
1/2 x 2/3 = (1 x 2) / (2 x 3) = 2/6
The fraction 2/6 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 2:
2/6 = 1/3
This concept expands the initial problem of 5 x 1/2 to more complex scenarios, providing a robust foundation for advanced mathematical concepts.
Conclusion: Mastering Fractions for a Brighter Future
This in-depth guide has provided a comprehensive exploration of calculating 5 x 1/2 as a fraction, going beyond the simple answer and delving into the underlying mathematical principles. We’ve covered multiple methods, visual representations, and practical applications, providing a strong foundation for understanding and working with fractions. Mastering fractions is crucial for success in various fields and for navigating the everyday mathematical challenges we encounter. By understanding the concepts discussed here, readers are empowered to approach more complex fraction problems with confidence and competence. Remember, the key to mastering fractions lies in consistent practice and a firm grasp of the fundamental concepts. With dedicated effort, anyone can achieve proficiency in this important area of mathematics.
Latest Posts
Latest Posts
-
How Many Days Is 17000 Minutes
May 25, 2025
-
How Many Hours In Three Months
May 25, 2025
-
What Is 100 To The Power Of 6
May 25, 2025
-
1 Out Of 22 As A Percentage
May 25, 2025
-
Buy New Or Used Car Calculator
May 25, 2025
Related Post
Thank you for visiting our website which covers about 5 X 1/2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.