1 1 2 4 3 9
listenit
May 26, 2025 · 5 min read
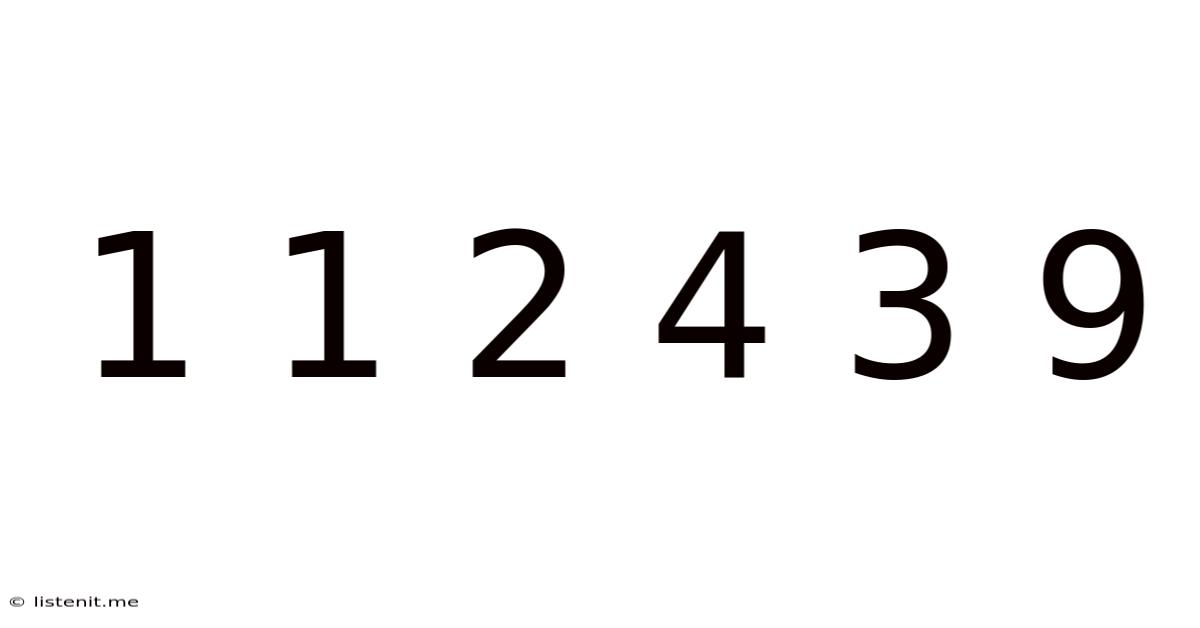
Table of Contents
Decoding the Sequence: 1 1 2 4 3 9 – Unveiling the Patterns and Possibilities
The seemingly simple sequence 1, 1, 2, 4, 3, 9… immediately sparks curiosity. It's not an arithmetic progression, nor a geometric one. What's the underlying rule? This article will delve into the fascinating world of number sequences, exploring various interpretations and potential patterns hidden within this intriguing series. We will examine different approaches to understanding the sequence, demonstrating how seemingly simple problems can open doors to complex mathematical concepts.
The Search for the Pattern: Beyond the Obvious
The immediate challenge lies in identifying the rule governing the progression from one number to the next. Simple addition or multiplication fails to reveal a consistent pattern. This suggests that the sequence might follow a more complex or recursive rule. Let's explore some possibilities:
A Potential Recursive Relationship:
One approach is to consider each number as potentially derived from the preceding numbers. Let's examine the differences between consecutive terms:
- 1 - 1 = 0
- 2 - 1 = 1
- 4 - 2 = 2
- 3 - 4 = -1
- 9 - 3 = 6
These differences don't immediately reveal a clear pattern either. However, let's consider the possibility of a more complex relationship involving multiple preceding terms. Perhaps each term is related to the sum or product of the previous terms, or even a combination of both. This opens up a broad range of potential rules, making the problem more challenging but also far more interesting.
Exploring Quadratic Relationships:
Another avenue of investigation involves examining if a quadratic relationship might exist. A quadratic equation relates the terms using a second-degree polynomial. While unlikely to fit this exact sequence perfectly, it might provide a reasonable approximation or hint at a more intricate pattern. Experimenting with various quadratic equations and their coefficients could potentially uncover an underlying quadratic trend.
The Role of Primes and Composites:
Let's also consider the properties of the numbers themselves. The sequence alternates between prime and composite numbers:
- 1 (neither prime nor composite)
- 1 (neither prime nor composite)
- 2 (prime)
- 4 (composite)
- 3 (prime)
- 9 (composite)
This alternation could be a clue, suggesting that the rule may involve the primality or compositeness of the numbers in some way. However, connecting this observation to a definitive rule still presents a significant challenge.
Advanced Mathematical Concepts and Their Potential Application:
The lack of an immediately obvious pattern necessitates exploring more advanced mathematical tools and techniques.
Generating Functions:
Generating functions are a powerful tool in combinatorics and number theory. They allow representing a sequence as a formal power series, where the coefficients correspond to the terms of the sequence. This representation can facilitate the identification of patterns and the derivation of closed-form expressions for the sequence's terms. However, applying generating functions to this specific sequence would require careful consideration and potentially advanced mathematical manipulations.
Recurrence Relations:
A recurrence relation defines each term of a sequence as a function of previous terms. For example, the Fibonacci sequence is defined by the recurrence relation F(n) = F(n-1) + F(n-2). While we have not found a simple recurrence relation for our sequence, a more complex one might exist, perhaps involving multiple previous terms or a non-linear function. Finding such a recurrence relation would require substantial mathematical experimentation and analysis.
Chaos Theory and Non-Linear Systems:
In some cases, seemingly random or unpredictable sequences can arise from deterministic but chaotic systems. While this might not be the case here, it's worth noting that the apparent lack of a simple pattern could indicate underlying complexity that requires more advanced methods of analysis rooted in chaos theory and the study of non-linear systems.
The Importance of Context and Further Data:
The analysis becomes significantly more fruitful if we know the context in which this sequence was presented. Where did this sequence originate? Is this the complete sequence, or are there more terms to follow? Additional data points would help clarify the pattern and validate or invalidate the hypotheses we've explored. The presence of additional terms would allow for a more robust statistical analysis and potentially reveal hidden correlations or regularities.
Exploring Alternative Interpretations:
The absence of an easily identifiable pattern could also suggest that the sequence might not follow a mathematical rule in the traditional sense. Perhaps the sequence represents an encoding, a code, or a stylized representation of a different kind of information. Considering this possibility opens up a broader range of interpretations:
A Code or Cipher:
Could this sequence be part of a larger code or cipher? Each number might represent a letter or symbol based on a specific coding scheme. Deciphering such a code would require additional clues or knowledge about the specific coding system used.
Data Encoding:
The sequence might represent some form of data encoding, where each number corresponds to a specific piece of information or a set of parameters. Understanding this encoding would necessitate context regarding the original data being represented.
The Value of Mathematical Exploration:
The quest to understand the sequence 1, 1, 2, 4, 3, 9... exemplifies the inherent beauty and challenge of mathematical exploration. The apparent simplicity of the problem belies the complexity and depth of the underlying mathematical principles involved. The process of investigation highlights the importance of considering different approaches, employing various analytical techniques, and acknowledging the limitations of our current knowledge.
Conclusion: A Journey of Mathematical Discovery
The sequence 1, 1, 2, 4, 3, 9… remains an intriguing puzzle. While we haven't definitively cracked its code, our exploration has showcased a wide array of mathematical tools and concepts, highlighting the richness and diversity of mathematical thinking. The process of investigation, rather than the final answer, is often the most rewarding aspect of such mathematical explorations. It teaches us to approach problems systematically, consider multiple perspectives, and appreciate the beauty of uncovering patterns and relationships in the seemingly random. Perhaps with additional information or a different perspective, the underlying rule will become clear. Until then, the mystery persists, inviting further investigation and stimulating further mathematical creativity. The journey of discovery is, in itself, a testament to the enduring allure of mathematics. This simple sequence serves as a powerful reminder of the vastness of mathematical possibilities and the boundless potential for uncovering hidden patterns and understanding the intricate workings of the universe.
Latest Posts
Latest Posts
-
Can Lack Of Sleep Cause Dizziness
May 27, 2025
-
What Type Of Conduction Takes Place In Unmyelinated Axons
May 27, 2025
-
What Is The Lowest Dose Of Hydrochlorothiazide
May 27, 2025
-
Reductive Glutamine Tracer M 1 Acetyl Coa
May 27, 2025
-
Pearson Correlation Between Weather Variables And Yield
May 27, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 4 3 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.