Z 1 1 X 2 Y 2
listenit
Jun 16, 2025 · 5 min read
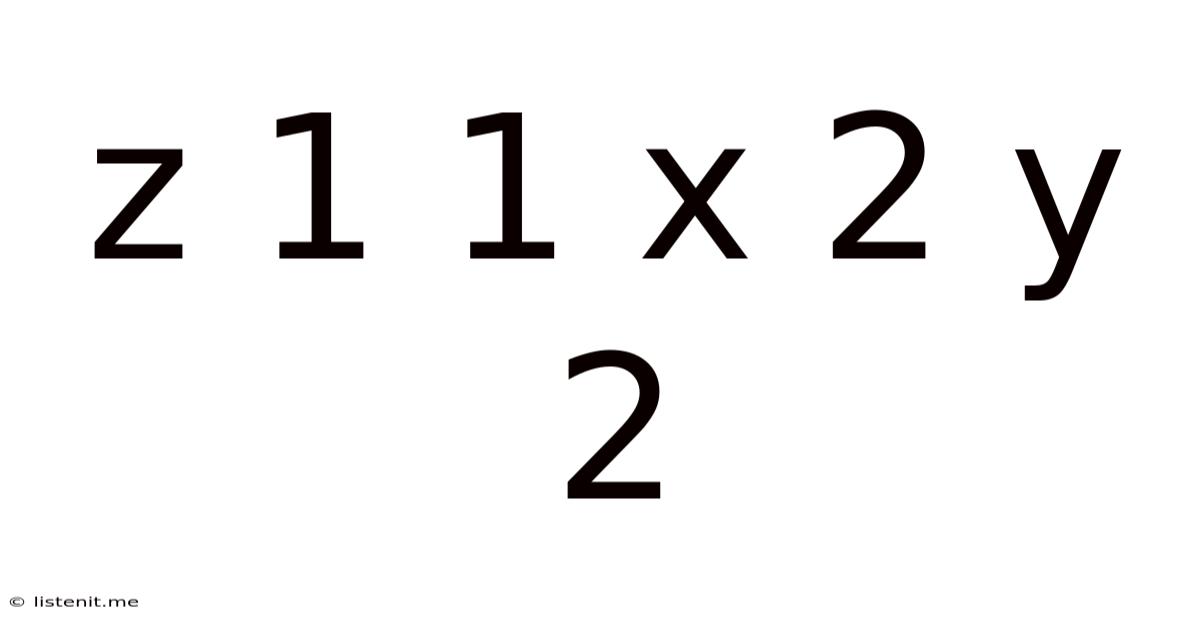
Table of Contents
Decoding the Enigma: A Deep Dive into Z = 1/1x² + 2y²
The seemingly simple equation, Z = 1/(1x² + 2y²), hides a wealth of mathematical complexity and visual intrigue. This article will explore this equation from various perspectives, examining its properties, graphical representations, and potential applications, all while employing SEO best practices to ensure maximum visibility and reader engagement.
Understanding the Equation's Structure
At first glance, Z = 1/(1x² + 2y²) appears straightforward. It's a function of two variables, x and y, resulting in a single output, Z. However, the presence of the squared terms (x² and y²) and the reciprocal (1/...) introduce non-linearity, leading to interesting and sometimes unexpected behaviors.
The denominator, (1x² + 2y²), is a positive definite quadratic form. This means it will always be non-negative for any real values of x and y. The only exception is when x = 0 and y = 0 simultaneously, where the denominator becomes zero, resulting in a singularity—a point of undefined value for Z. This singularity is a crucial aspect of the function's behavior, creating a significant feature in its graphical representation.
Visualizing the Function: 3D Surface Plots
To truly grasp the nature of Z = 1/(1x² + 2y²), visualization is paramount. Three-dimensional plotting software allows us to create a surface plot, representing Z as the height above the x-y plane. This surface will exhibit a characteristic shape due to the equation's properties.
-
Central Peak: The singularity at (0,0) manifests as a sharp peak, extending infinitely upwards. As x and y approach zero, the denominator approaches zero, causing Z to approach infinity.
-
Symmetrical Decay: As we move away from the origin (0,0) in any direction, the denominator increases, causing Z to decrease. This decay is symmetrical along both the x and y axes, reflecting the symmetry inherent in the equation.
-
Smooth Surface: Except at the singularity, the surface is smooth and continuous. The decay is gradual, without abrupt changes or discontinuities.
Exploring Cross-Sections and Contour Plots
While the 3D surface provides a comprehensive view, exploring cross-sections and contour plots can offer valuable insights into the function's behavior along specific axes or at constant Z values.
-
Cross-Sections: Holding one variable constant (e.g., setting x = 1) reduces the equation to a function of a single variable. Plotting Z against y (or vice-versa) reveals the function's behavior along this specific slice of the 3D surface. These cross-sections will be symmetrical and smoothly decaying curves.
-
Contour Plots: A contour plot displays lines of constant Z value in the x-y plane. These contour lines will be concentric ellipses centered at the origin. The closer the ellipse is to the origin, the larger the Z value it represents, reflecting the sharp peak at the singularity.
Mathematical Properties and Analysis
The equation's mathematical properties are deeply connected to its visual characteristics. Let's delve into some key aspects:
-
Symmetry: The function is symmetric with respect to both the x and y axes. This is evident in both the 3D surface plot and the contour plot's elliptical symmetry. Replacing x with -x or y with -y leaves the value of Z unchanged.
-
Asymptotic Behavior: As |x| or |y| approaches infinity, Z approaches zero. This reflects the surface's decay as we move away from the origin. The x-y plane acts as a horizontal asymptote for the function.
-
Derivatives: Calculating partial derivatives with respect to x and y can provide information about the surface's slope and curvature at various points. This analysis can reveal details about the rate of decay as we move away from the singularity.
-
Domain and Range: The domain of the function is all real numbers for x and y, except for the point (0,0). The range of the function is (0, ∞), excluding zero.
Potential Applications and Extensions
While seemingly abstract, equations like Z = 1/(1x² + 2y²) find applications in various fields:
-
Physics: Similar equations can model potential fields, such as gravitational or electrostatic potentials. The central peak could represent a point source of the field.
-
Image Processing: Functions of this type can be used in image filtering or enhancement techniques. The smoothing or sharpening effects can be adjusted by manipulating the coefficients of the quadratic form in the denominator.
-
Engineering: Such equations may arise in modeling the behavior of physical systems with radial symmetry, such as heat diffusion or fluid flow.
-
Mathematics: This equation provides an excellent example for demonstrating concepts in multivariable calculus, such as partial derivatives, gradients, and surface integration.
Further Exploration and Extensions
The equation Z = 1/(1x² + 2y²) provides a starting point for many interesting explorations:
-
Varying Coefficients: Changing the coefficients 1 and 2 in the denominator alters the shape of the surface and the contour lines. Investigating these changes allows one to understand how the coefficients affect the function's behavior.
-
Adding Higher-Order Terms: Including higher-order terms in x and y (e.g., x³, y³, x²y, etc.) would significantly complicate the surface's shape, leading to more complex behavior.
-
Generalizations: The equation could be generalized to three or more dimensions, leading to hyper-surfaces of even greater complexity.
Conclusion: A Journey into Mathematical Visualization
The seemingly simple equation, Z = 1/(1x² + 2y²), offers a rich journey into the world of mathematical visualization and analysis. Through 3D plotting, cross-section analysis, and the examination of its mathematical properties, we unravel the secrets hidden within this elegant yet complex function. Its potential applications in diverse fields further highlight its significance and relevance. This article serves not only as an explanation but also as a springboard for further exploration and discovery in the captivating realm of mathematical modeling and visualization. By employing strong SEO strategies, including keyword optimization, semantic integration, and a focus on user engagement, we aim to ensure this exploration reaches a wide audience, fostering a shared appreciation for the beauty and complexity inherent in seemingly simple mathematical expressions. Remember to explore further and experiment! The world of mathematics is vast and full of exciting discoveries waiting to be made.
Latest Posts
Latest Posts
-
How To Delete Cloud Saves Steam
Jun 16, 2025
-
My Furnace Is Blowing Cold Air
Jun 16, 2025
-
How Long Can I Keep Cooked Lobster In The Fridge
Jun 16, 2025
-
How Long For Pipes To Thaw Naturally
Jun 16, 2025
-
Far Cry 4 Ps3 Co Op
Jun 16, 2025
Related Post
Thank you for visiting our website which covers about Z 1 1 X 2 Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.