What's The Square Root Of 37
listenit
Apr 02, 2025 · 5 min read
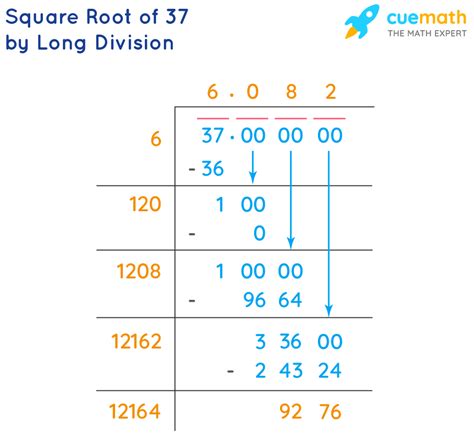
Table of Contents
What's the Square Root of 37? A Deep Dive into Irrational Numbers and Approximation Methods
The seemingly simple question, "What's the square root of 37?", opens a fascinating exploration into the world of mathematics, specifically concerning irrational numbers and the various methods used to approximate their values. While a precise answer isn't readily available as a simple fraction or decimal, understanding the approaches to finding its value provides valuable insights into mathematical concepts and computational techniques.
Understanding Square Roots and Irrational Numbers
Before diving into the methods of calculating the square root of 37, let's establish a foundational understanding of square roots and irrational numbers.
What is a Square Root? The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3, because 3 * 3 = 9.
What are Irrational Numbers? Irrational numbers are real numbers that cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representations are non-terminating (they don't end) and non-repeating (they don't have a continuously repeating pattern). Many square roots of non-perfect squares are irrational numbers. Since 37 is not a perfect square (no whole number multiplied by itself equals 37), its square root is an irrational number.
Methods for Approximating √37
Given that √37 is irrational, we cannot find its exact value. However, we can use various methods to approximate it to a desired level of accuracy.
1. The Babylonian Method (or Heron's Method)
This iterative method refines an initial guess to progressively closer approximations of the square root.
Steps:
- Make an initial guess: Let's start with a guess of 6, as 6 * 6 = 36, which is close to 37.
- Refine the guess: Divide the number (37) by the initial guess (6): 37/6 ≈ 6.1667
- Average: Average the initial guess and the result from step 2: (6 + 6.1667)/2 ≈ 6.0833
- Repeat: Use the result from step 3 as the new guess and repeat steps 2 and 3. The more iterations you perform, the closer you get to the actual value.
Let's perform a few iterations:
- Iteration 1: Guess = 6, 37/6 ≈ 6.1667, Average ≈ 6.0833
- Iteration 2: Guess = 6.0833, 37/6.0833 ≈ 6.0827, Average ≈ 6.0830
- Iteration 3: Guess = 6.0830, 37/6.0830 ≈ 6.0828, Average ≈ 6.0829
After just a few iterations, we've already reached a very close approximation of √37 ≈ 6.0829.
2. Using a Calculator or Computer Software
The simplest method for approximating √37 is using a calculator or computer software with a built-in square root function. These tools employ sophisticated algorithms to calculate the square root to a high degree of precision. Most calculators will give you a result like 6.082762530298219...
3. Linear Approximation
This method uses the tangent line to approximate the square root. While less precise than the Babylonian method, it's conceptually simpler.
Consider the function f(x) = √x. We can find the tangent line at a point close to 37, say at x=36 (since √36 = 6). The derivative of f(x) is f'(x) = 1/(2√x). At x=36, f'(36) = 1/(2*6) = 1/12.
The equation of the tangent line at x=36 is:
y - 6 = (1/12)(x - 36)
Substituting x = 37, we get:
y - 6 = (1/12)(1) => y ≈ 6.0833
This linear approximation gives a reasonably close result, although less accurate than the Babylonian method.
4. Newton-Raphson Method
This is another iterative method, similar to the Babylonian method, but it's based on the derivative of a function. For finding the square root of a number 'a', the iterative formula is:
x_(n+1) = 0.5 * (x_n + a/x_n)
where x_n is the current approximation and x_(n+1) is the next approximation. This method converges to the solution quickly.
5. Continued Fractions
This method represents the square root as a continued fraction, an expression of the form:
a_0 + 1/(a_1 + 1/(a_2 + 1/(a_3 + ...)))
Finding the continued fraction representation for √37 involves a process of finding the integer part and the reciprocal of the remaining fractional part repeatedly. While theoretically elegant, calculating continued fractions can be cumbersome for higher precision.
The Significance of Irrational Numbers
The fact that √37 is irrational highlights the richness and complexity of the number system. Irrational numbers, though seemingly inconvenient because they cannot be expressed exactly as fractions, are fundamental to mathematics and have countless applications in various fields.
- Geometry: Irrational numbers often appear in geometric calculations, such as the diagonal of a square (√2), the circumference of a circle (π), and the golden ratio (φ).
- Physics: Many physical phenomena involve irrational numbers, appearing in formulas and equations describing wave motion, oscillations, and other natural processes.
- Engineering: Precise calculations in engineering often necessitate the use of approximations of irrational numbers to achieve desired levels of accuracy.
Conclusion
Approximating the square root of 37, while not yielding a perfectly precise answer, offers a valuable opportunity to explore different mathematical concepts and computational techniques. From the iterative methods like the Babylonian and Newton-Raphson methods to simpler linear approximations and the use of calculators, several approaches provide increasingly accurate estimations. The exploration itself underscores the importance of irrational numbers and their significant role across various scientific disciplines. Understanding these methods enhances mathematical intuition and appreciation for the beauty and complexity of the number system. The journey to approximate √37 is not just about finding a numerical answer; it's a journey into the heart of mathematical reasoning and computation.
Latest Posts
Latest Posts
-
What Is The Shape Of The Orbits Of The Planets
Apr 03, 2025
-
1 1 2 Tablespoons Divided By 2
Apr 03, 2025
-
Lowest Common Multiple Of 25 And 35
Apr 03, 2025
-
Is Square Root Of 16 A Rational Number
Apr 03, 2025
-
What Is 6 8 As A Decimal
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 37 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
