Is Square Root Of 16 A Rational Number
listenit
Apr 03, 2025 · 5 min read
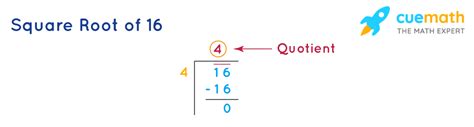
Table of Contents
Is the Square Root of 16 a Rational Number? A Deep Dive into Rationality and Irrationality
The question, "Is the square root of 16 a rational number?" might seem deceptively simple at first glance. However, understanding the answer requires a firm grasp of fundamental mathematical concepts, specifically rational and irrational numbers. This article will not only answer this specific question definitively but also delve into the broader context of number systems, exploring the characteristics that distinguish rational numbers from their irrational counterparts. We'll also explore practical applications and further expand on the concepts for a deeper understanding.
Understanding Rational Numbers
Before tackling the square root of 16, let's establish a clear definition of a rational number. A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p is the numerator and q is the denominator, and q is not zero. Crucially, this fraction must be able to be simplified to a terminating or repeating decimal.
Examples of Rational Numbers:
- 1/2: This is a simple fraction representing 0.5.
- 3/4: This fraction equals 0.75.
- -2/5: This is equal to -0.4.
- 7: The integer 7 can be expressed as 7/1, fulfilling the definition.
- 0.333...: This repeating decimal is equivalent to 1/3.
- 2.75: This terminating decimal can be written as 11/4.
Understanding Irrational Numbers
In contrast to rational numbers, irrational numbers cannot be expressed as a simple fraction of two integers. Their decimal representations are non-terminating and non-repeating. This means the decimal goes on forever without ever settling into a repeating pattern.
Examples of Irrational Numbers:
- π (pi): The ratio of a circle's circumference to its diameter, approximately 3.14159... but continuing infinitely without repetition.
- √2 (the square root of 2): Approximately 1.41421356..., its decimal representation is non-terminating and non-repeating.
- e (Euler's number): The base of the natural logarithm, approximately 2.71828..., also non-terminating and non-repeating.
- The golden ratio (φ): Approximately 1.61803398..., another irrational number with significant mathematical properties.
Calculating the Square Root of 16
Now, let's focus on the core question: Is √16 a rational number? The square root of a number is a value that, when multiplied by itself, gives the original number. In this case, we're looking for a number that, when multiplied by itself, equals 16.
The answer is 4. Because 4 multiplied by itself (4 x 4) equals 16.
Is 4 a Rational Number?
The next step is to determine if 4 is a rational number based on our definition. Can 4 be expressed as a fraction p/q, where p and q are integers and q is not zero? Absolutely! 4 can be written as 4/1, 8/2, 12/3, and so on. Since 4 satisfies the definition of a rational number, the answer to our initial question is a resounding yes.
Further Exploration of Rational and Irrational Numbers
The distinction between rational and irrational numbers is fundamental in mathematics. Many mathematical concepts and theorems rely on this classification. For instance:
-
Real Numbers: Rational and irrational numbers together comprise the set of real numbers. Real numbers encompass all numbers on the number line.
-
Decimal Representation: The decimal representation provides a practical way to distinguish between rational and irrational numbers. Rational numbers have either terminating or repeating decimals, while irrational numbers have non-terminating and non-repeating decimals.
-
Proofs of Irrationality: Proving a number is irrational often requires sophisticated mathematical techniques. Famous proofs exist for the irrationality of √2, π, and e. These proofs typically utilize proof by contradiction.
-
Approximations: While we can't express irrational numbers exactly as fractions, we can approximate them using rational numbers with increasing accuracy. This is crucial in many applications where precise calculations are impractical.
-
Continued Fractions: Irrational numbers can often be represented as continued fractions, offering another way to express them and analyze their properties. Continued fractions are a powerful tool in number theory.
Practical Applications of Rational and Irrational Numbers
Rational and irrational numbers are not just abstract mathematical concepts; they have practical applications across various fields:
-
Engineering and Construction: Rational numbers are used extensively in engineering calculations and measurements. Precise dimensions and ratios are essential for building structures.
-
Computer Science: While computers work with finite precision, they often need to handle both rational and approximations of irrational numbers. Algorithms for dealing with irrational numbers are crucial for tasks like graphics rendering and scientific simulations.
-
Finance: Rational numbers are fundamental in financial calculations, dealing with monetary values, interest rates, and asset pricing.
-
Physics: Irrational numbers, such as pi, appear naturally in physics when dealing with circles, spheres, and other curved shapes.
-
Everyday Life: We encounter rational numbers frequently in daily life – measuring ingredients, calculating distances, and managing finances. While we may not explicitly think about it, rational numbers are essential for our daily activities.
Beyond the Square Root of 16: Exploring Other Examples
Let's consider a few more examples to solidify our understanding of rational and irrational numbers:
- √9: This is equal to 3, a rational number (3/1).
- √25: This is equal to 5, also a rational number (5/1).
- √2: This is an irrational number, its decimal representation is non-terminating and non-repeating.
- √7: Another irrational number.
- √100: This equals 10, a rational number (10/1).
Notice a pattern? The square roots of perfect squares (numbers that are the result of squaring an integer) are always rational. The square roots of non-perfect squares are always irrational.
Conclusion: Rationality and its Significance
The question of whether the square root of 16 is a rational number has led us on a journey through the fascinating world of number systems. We have established that √16, which is 4, is indeed a rational number because it can be expressed as the fraction 4/1. This seemingly simple example serves as a gateway to understanding the broader implications of rationality and irrationality in mathematics and its applications. Understanding the difference between rational and irrational numbers is crucial for further mathematical study and for countless applications across various disciplines. The distinctions between these number types are fundamental building blocks for more advanced mathematical concepts and real-world problem-solving.
Latest Posts
Latest Posts
-
How Much Is 9 Ounces In Cups
Apr 04, 2025
-
Describe The Function Of The Lens
Apr 04, 2025
-
What Are The Two Strands Of Dna Held Together By
Apr 04, 2025
-
How Many Atoms Of Oxygen Are In H2o
Apr 04, 2025
-
Do Homologous Chromosomes Have The Same Alleles
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Is Square Root Of 16 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
