What's The Square Root Of 23
listenit
Mar 29, 2025 · 5 min read
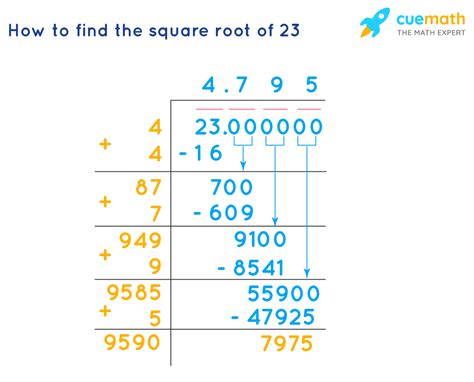
Table of Contents
What's the Square Root of 23? A Deep Dive into Irrational Numbers
The seemingly simple question, "What's the square root of 23?" opens a door to a fascinating world of mathematics, specifically the realm of irrational numbers. While a quick search on a calculator will give you a decimal approximation, understanding the true nature of √23 requires a deeper exploration. This article will delve into the intricacies of this specific square root, examining its properties, methods of approximation, and its significance within the broader mathematical landscape.
Understanding Square Roots and Irrational Numbers
Before we tackle √23, let's establish a foundational understanding. The square root of a number (x) is a value that, when multiplied by itself, equals x. In simpler terms, it's the inverse operation of squaring a number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9.
However, not all square roots are whole numbers. Numbers like √2, √3, and our subject, √23, are irrational numbers. This means they cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representations are non-terminating and non-repeating; they go on forever without ever settling into a predictable pattern. This is a fundamental property that distinguishes them from rational numbers like 1/2 or 0.75.
Approximating √23: Methods and Techniques
Since √23 is irrational, we cannot find its exact value. Instead, we rely on approximation methods. Several techniques can help us determine a close estimate:
1. Using a Calculator: The Quick and Easy Method
The most straightforward approach is to use a calculator. A scientific calculator will readily provide an approximation of √23, typically to several decimal places (e.g., 4.79583152331). While convenient, this method doesn't offer insight into the underlying mathematical processes.
2. The Babylonian Method (or Heron's Method): An Iterative Approach
The Babylonian method is an ancient algorithm for calculating square roots iteratively. It refines an initial guess through repeated calculations, converging closer to the actual value with each iteration. Here's how it works for √23:
-
Start with an initial guess: Let's guess 5, as 5² = 25, which is close to 23.
-
Improve the guess: Divide the number (23) by the guess (5): 23/5 = 4.6
-
Average the guess and the result: (5 + 4.6) / 2 = 4.8
-
Repeat steps 2 and 3:
- 23/4.8 ≈ 4.791667
- (4.8 + 4.791667) / 2 ≈ 4.795833
-
Continue iterating: With each iteration, the approximation gets closer to the actual value of √23. The more iterations you perform, the higher the accuracy.
This method demonstrates a powerful iterative process that converges towards the solution. It’s a fundamental algorithm used in various numerical computations.
3. Linear Approximation: Using Nearby Perfect Squares
Another approach involves using nearby perfect squares. Since 4² = 16 and 5² = 25, √23 lies between 4 and 5. We can estimate its position by considering the distances:
- 23 - 16 = 7
- 25 - 23 = 2
The distance to 16 is greater than the distance to 25, suggesting √23 is closer to 5 than 4. A simple linear interpolation gives a rough approximation:
4 + (2/9) ≈ 4.22
While less precise than the Babylonian method, this approach provides a quick, intuitive estimate.
The Significance of √23 and Irrational Numbers
The seemingly insignificant √23 holds a significant place within mathematics. Its irrationality highlights the richness and complexity of the number system. Irrational numbers, though seemingly abstract, have practical implications across various fields:
-
Geometry: Irrational numbers frequently arise in geometrical calculations, especially when dealing with circles and triangles (e.g., the Pythagorean theorem). The diagonal of a square with sides of length 1 is √2, a classic example of an irrational number’s geometrical relevance.
-
Physics: Many physical phenomena involve irrational numbers. For instance, the ratio of a circle's circumference to its diameter (π) is an irrational number, essential for understanding circular motion and wave phenomena.
-
Computer Science: Approximating irrational numbers is a crucial aspect of computer algorithms and simulations. The accuracy of these approximations directly impacts the precision of computational results.
-
Engineering: Precise calculations involving irrational numbers are vital in various engineering disciplines, ensuring accurate designs and constructions.
Beyond √23: Exploring Other Irrational Numbers
Understanding √23 helps us appreciate the broader category of irrational numbers. Other notable examples include:
-
π (Pi): The ratio of a circle's circumference to its diameter, approximately 3.14159.
-
e (Euler's number): The base of the natural logarithm, approximately 2.71828.
-
The Golden Ratio (φ): Approximately 1.61803, appearing in art, architecture, and natural phenomena.
These irrational numbers, along with countless others, demonstrate the infinite richness and complexity of the real number system. Their exploration leads to a deeper appreciation of mathematics' elegance and its practical applications across numerous scientific and engineering fields.
Conclusion: Embracing the Irrational
The square root of 23, while seemingly a simple mathematical concept, encapsulates the essence of irrational numbers. Its precise value remains elusive, emphasizing the need for approximation methods. Through exploring different techniques, we not only find numerical estimates but also gain insights into fundamental mathematical principles and algorithms. The significance of √23 extends beyond its numerical value; it's a testament to the beauty and complexity of mathematics and its crucial role in understanding and shaping our world. The journey of calculating and understanding √23 serves as a microcosm of the ongoing exploration of irrational numbers and their enduring influence across various disciplines. Understanding its nature helps us appreciate the intricate tapestry of mathematics and its vital role in our world.
Latest Posts
Latest Posts
-
The Elbow Is Distal To The Wrist
Mar 31, 2025
-
What Do Coefficients Represent In A Chemical Equation
Mar 31, 2025
-
Why Do Chemical Equations Have To Be Balanced
Mar 31, 2025
-
What Percent Is A 26 Out Of 30
Mar 31, 2025
-
Which Is Denser Oceanic Or Continental Crust
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 23 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
