What Percent Is 4 Of 15
listenit
May 25, 2025 · 5 min read
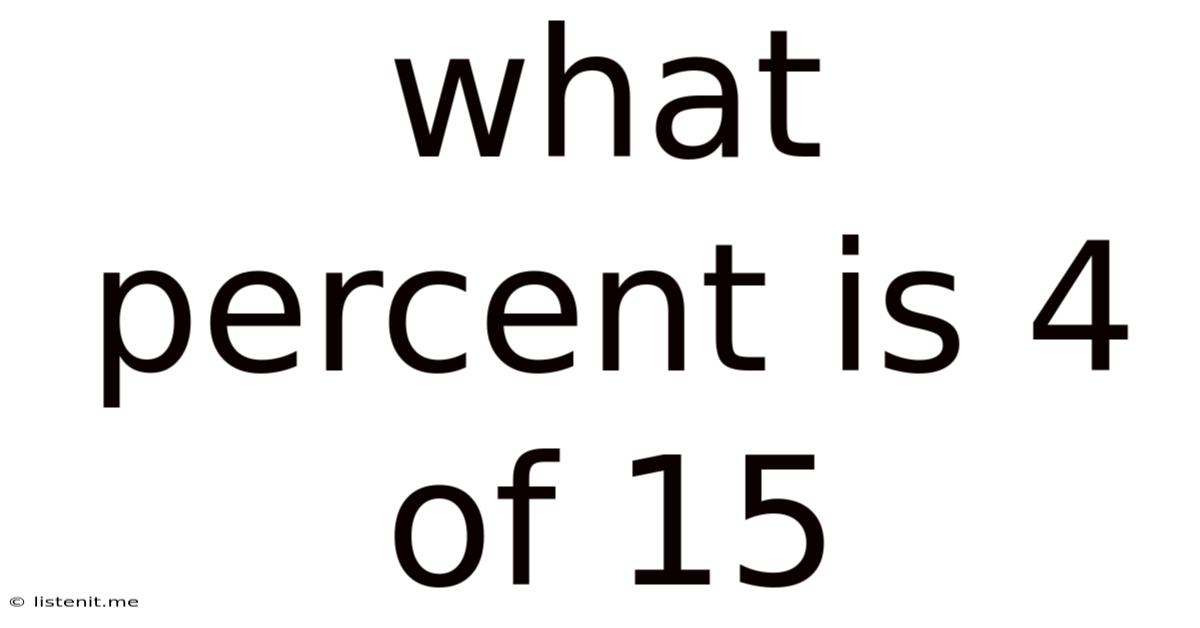
Table of Contents
What Percent is 4 of 15? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in everyday life, from understanding sales discounts to analyzing financial data. This article delves into the seemingly simple question, "What percent is 4 of 15?", providing a comprehensive explanation of the process, exploring different calculation methods, and demonstrating its practical relevance across various scenarios.
Understanding Percentages: The Basics
Before we tackle the specific problem, let's establish a solid understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "percent" or "out of 100." Essentially, a percentage represents a portion of a whole. For example, 50% means 50 out of 100, which is equivalent to one-half (½) or 0.5 as a decimal.
Method 1: The Formula Approach
The most straightforward way to determine what percent 4 is of 15 is to use the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 4 (the number we're interested in finding the percentage of)
- Whole: 15 (the total amount)
Substituting these values into the formula:
(4 / 15) x 100% = Percentage
This calculation yields:
0.266666... x 100% ≈ 26.67%
Therefore, 4 is approximately 26.67% of 15. The slight rounding is common when dealing with percentages, as the result is often a non-terminating decimal.
Method 2: Proportion Method
Another effective method involves setting up a proportion. This approach highlights the relationship between the parts and the whole. We can represent the problem as:
4 / 15 = x / 100
Here, 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
4 x 100 = 15x
400 = 15x
x = 400 / 15
x ≈ 26.67
Again, we arrive at the same approximate answer: 26.67%. This method reinforces the conceptual understanding of percentages as ratios.
Method 3: Using Decimal Conversion
We can also solve this by first converting the fraction 4/15 into a decimal and then multiplying by 100%:
4 ÷ 15 ≈ 0.2667
0.2667 x 100% ≈ 26.67%
This method is particularly useful when working with a calculator, as it streamlines the calculation process.
Practical Applications: Real-World Scenarios
Understanding percentage calculations isn't just about solving mathematical problems; it has significant practical implications across various fields. Here are a few examples:
1. Sales and Discounts
Imagine a store offering a discount. If an item is originally priced at $15 and is discounted by $4, the discount percentage is calculated as:
(4 / 15) x 100% ≈ 26.67%
This signifies that the item is being sold at a 26.67% discount.
2. Financial Analysis
Percentage calculations are essential for interpreting financial statements. For instance, if a company's profit is $4 million out of a total revenue of $15 million, its profit margin is:
(4 / 15) x 100% ≈ 26.67%
This indicates that the company's profit margin is approximately 26.67%. Analyzing such metrics helps assess a company's financial health and performance.
3. Grade Calculations
Percentage calculations are fundamental in educational settings. Suppose a student scores 4 points out of a possible 15 points on a quiz. Their score as a percentage is:
(4 / 15) x 100% ≈ 26.67%
This shows that the student achieved approximately a 26.67% on the quiz.
4. Statistics and Data Analysis
Percentages are ubiquitous in statistical analysis. For example, if 4 out of 15 participants in a survey responded positively to a particular question, the percentage of positive responses is:
(4 / 15) x 100% ≈ 26.67%
This data point is essential for interpreting survey results and drawing meaningful conclusions.
5. Everyday Life
Numerous everyday situations involve percentage calculations. For example, determining the percentage of a tip in a restaurant, calculating the percentage of ingredients in a recipe, or even figuring out the percentage of completion on a project.
Beyond the Basics: Advanced Percentage Calculations
While the problem "What percent is 4 of 15?" provides a basic understanding of percentage calculations, there are more complex scenarios requiring advanced techniques. These include:
-
Calculating percentage increase or decrease: This involves finding the percentage change between two values. For example, if a value increases from 15 to 19, the percentage increase is calculated as [(19-15)/15] x 100% = 26.67%.
-
Finding the original value after a percentage change: If a value is increased by 20% to reach 18, we can use algebra to find the original value.
-
Working with compound percentages: This involves calculating percentages on percentages, often seen in compound interest calculations.
-
Solving percentage word problems: These problems often require a clear understanding of the problem statement to correctly identify the part and the whole.
Mastering these advanced concepts requires practice and a strong understanding of algebraic principles. Numerous online resources and textbooks can provide further guidance.
Conclusion: The Power of Percentage Calculations
The seemingly simple question, "What percent is 4 of 15?", unveils the fundamental importance of percentage calculations in various aspects of our lives. From financial analysis and data interpretation to everyday decision-making, understanding how to calculate percentages empowers us to make informed choices and interpret data effectively. By mastering different calculation methods and expanding our knowledge to encompass more complex scenarios, we can leverage the power of percentages to navigate the complexities of the modern world. Remember the core formula, (Part/Whole) x 100%, and practice regularly to solidify your understanding. This skill will serve you well in countless situations throughout your life.
Latest Posts
Latest Posts
-
What Is 3 5 Of 60
May 25, 2025
-
Round 337 535169831 To The Nearest Ten
May 25, 2025
-
Highest Common Factor Of 40 And 30
May 25, 2025
-
What Is 2 3 Of 400
May 25, 2025
-
Date Of Birth To Be 18
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 4 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.