What Is 3 5 Of 60
listenit
May 25, 2025 · 4 min read
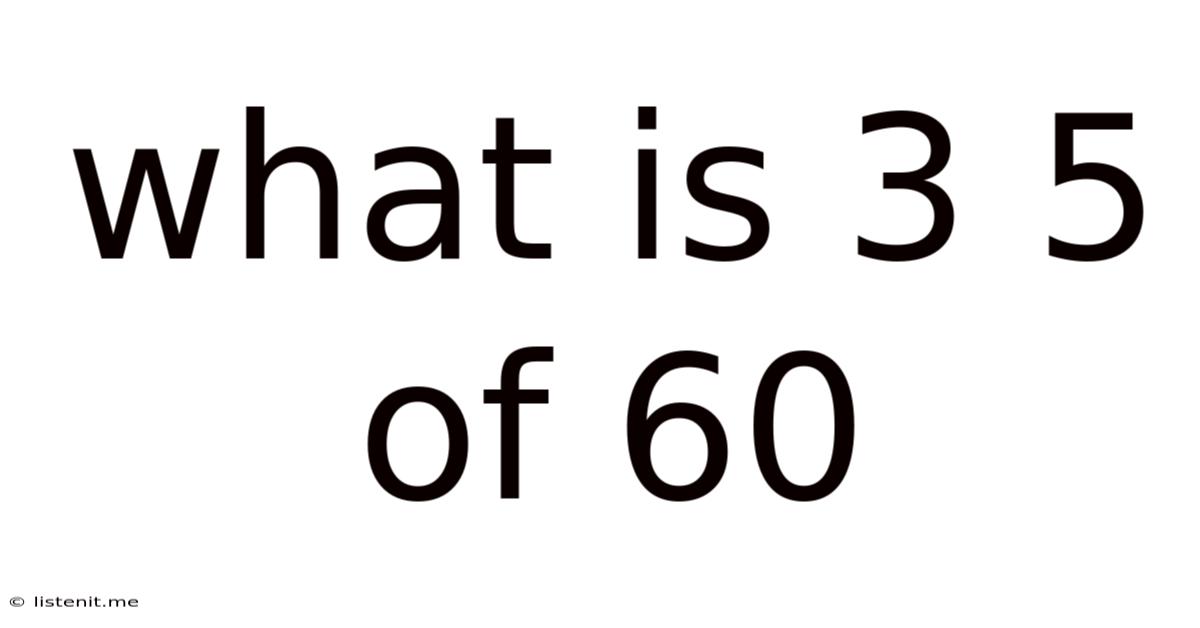
Table of Contents
What is 3/5 of 60? A Comprehensive Guide to Fractions and Percentages
Understanding fractions and percentages is crucial for everyday life, from calculating discounts to understanding financial reports. This article will delve into the question, "What is 3/5 of 60?", providing a step-by-step solution and exploring the broader concepts involved. We'll also cover various methods for solving similar problems, ensuring you gain a firm grasp of these fundamental mathematical operations.
Understanding Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts the whole is divided into. In our case, 3/5 means we have 3 parts out of a total of 5 parts.
Key Fraction Concepts
- Numerator: The top number (3 in 3/5). This represents the number of parts considered.
- Denominator: The bottom number (5 in 3/5). This represents the total number of equal parts.
- Proper Fraction: A fraction where the numerator is less than the denominator (e.g., 3/5, 1/2).
- Improper Fraction: A fraction where the numerator is greater than or equal to the denominator (e.g., 5/3, 4/4).
- Mixed Number: A combination of a whole number and a proper fraction (e.g., 1 2/3).
Solving "What is 3/5 of 60?"
To find 3/5 of 60, we need to perform a simple multiplication. There are two main approaches:
Method 1: Direct Multiplication
This is the most straightforward method. We multiply the fraction (3/5) by the whole number (60):
(3/5) * 60 = (3 * 60) / 5 = 180 / 5 = 36
Therefore, 3/5 of 60 is 36.
Method 2: Finding the Value of One-Fifth
This method involves breaking down the problem into smaller, more manageable steps. First, we find the value of one-fifth (1/5) of 60:
60 / 5 = 12
Since 1/5 of 60 is 12, we can then multiply this value by 3 to find 3/5 of 60:
12 * 3 = 36
Again, we arrive at the answer: 3/5 of 60 is 36.
Converting Fractions to Percentages
Fractions and percentages are closely related. A percentage is simply a fraction where the denominator is 100. To convert a fraction to a percentage, we multiply the fraction by 100%:
(3/5) * 100% = (3 * 100) / 5 % = 300 / 5 % = 60%
This tells us that 3/5 is equivalent to 60%. Therefore, finding 60% of 60 would also give us the same answer:
60% of 60 = (60/100) * 60 = 0.6 * 60 = 36
Real-World Applications
Understanding how to calculate fractions and percentages is essential in many real-world scenarios:
1. Shopping Discounts:
Imagine a store offering a 3/5 discount on an item priced at $60. Using our calculations, the discount would be $36, and the final price would be $60 - $36 = $24.
2. Financial Calculations:
Calculating interest, taxes, or profit margins often involves working with fractions and percentages. For example, if you earn a 3/5 commission on sales, you can easily calculate your earnings based on your sales figures.
3. Recipe Adjustments:
When cooking, you might need to adjust recipes based on the number of servings. If a recipe calls for 3/5 of a cup of flour but you want to double the recipe, you would calculate (3/5) * 2 = 6/5 or 1 1/5 cups of flour.
4. Data Analysis:
In data analysis, representing data as fractions or percentages simplifies understanding and comparing different proportions. For instance, if 3/5 of survey respondents preferred a certain product, it's easier to visualize this as 60% preference.
Practice Problems
To solidify your understanding, try solving these problems:
- What is 2/3 of 90?
- What is 4/7 of 140?
- Convert 5/8 into a percentage.
- Find 15% of 200.
- If a shirt is $75 and has a 2/5 discount, what is the final price?
Advanced Concepts: Working with More Complex Fractions
While the example "3/5 of 60" involved a simple fraction, the principles remain the same for more complex calculations. Consider scenarios involving mixed numbers or improper fractions.
For example, let's find 1 1/2 of 40:
First, convert the mixed number to an improper fraction: 1 1/2 = (1*2 + 1)/2 = 3/2
Now, multiply: (3/2) * 40 = 120/2 = 60
Thus, 1 1/2 of 40 is 60.
Conclusion
Mastering the calculation of fractions and percentages is a valuable skill for navigating various aspects of daily life. This article provided a detailed explanation of how to determine "What is 3/5 of 60?", explored different methods of calculation, highlighted the connection between fractions and percentages, and showed real-world applications. By understanding and practicing these fundamental mathematical operations, you will enhance your problem-solving abilities and confidently tackle numerous numerical challenges. Remember, consistent practice is key to building a strong foundation in these essential mathematical concepts. Keep practicing, and you'll find that working with fractions and percentages becomes increasingly intuitive and effortless.
Latest Posts
Latest Posts
-
What Percent Is 27 Out Of 35
May 25, 2025
-
What Is The Volume Of The Cylinder Below 8 4
May 25, 2025
-
How Old Am I If Im Born In 1965
May 25, 2025
-
How Many Months In 23 Years
May 25, 2025
-
Find The Surface Area Of The Following Figure
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 5 Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.