What Is The Value Of X 14 15 16 17
listenit
May 23, 2025 · 5 min read
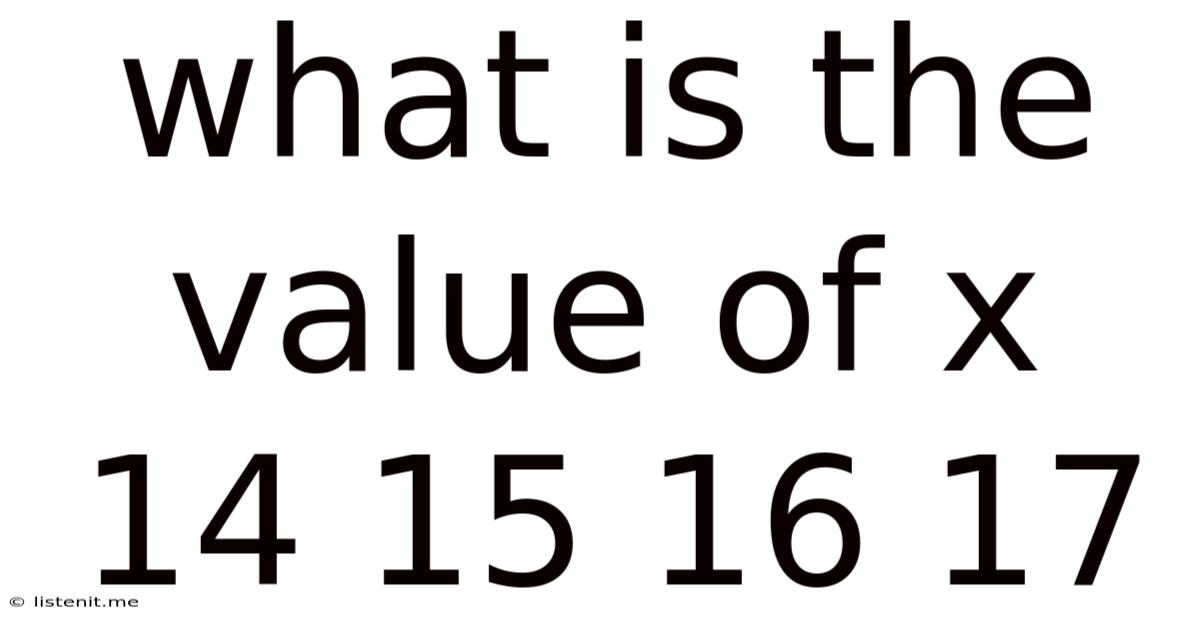
Table of Contents
Unlocking the Mystery: What is the Value of x in the Sequence 14, 15, 16, 17? A Deep Dive into Number Patterns and Problem-Solving
This seemingly simple question, "What is the value of x in the sequence 14, 15, 16, 17?", opens the door to a fascinating exploration of number patterns, mathematical reasoning, and the importance of context in problem-solving. While the immediate answer might seem obvious to some, a deeper dive reveals the multifaceted nature of such questions and the crucial role of assumptions in finding solutions.
The Obvious Answer: A Simple Arithmetic Sequence
At first glance, the sequence 14, 15, 16, 17 exhibits a clear pattern: each number is one more than the preceding number. This indicates an arithmetic sequence with a common difference of 1. Therefore, if 'x' represents the next number in the sequence, the most straightforward answer is:
x = 18
This solution is based on the assumption that the pattern continues linearly and consistently. This assumption is often implicitly made when dealing with numerical sequences, particularly in introductory mathematics problems. However, the beauty of mathematics lies in its ability to embrace multiple interpretations and perspectives.
Beyond the Obvious: Challenging Assumptions and Exploring Alternatives
While the arithmetic sequence provides a simple and satisfying solution, it's crucial to consider that other possibilities exist. The provided sequence is short, and a short sequence can be compatible with multiple patterns. Let's explore some alternative interpretations:
1. A Finite Sequence with a Hidden Meaning:
The sequence might not be part of a larger, ongoing pattern. It could be a purposefully chosen subset of numbers with a specific meaning or context. For instance, these numbers could represent:
- Days in a particular week (starting from Sunday): If the sequence started on Sunday, 14 could represent Sunday, and 17 would be Wednesday, leading to different interpretations for ‘x’.
- Specific dates: The numbers could represent days of a month, parts of an address, or elements in a code. Without additional context, any interpretation is plausible.
2. A Sequence with a Non-linear Pattern:
We assumed a linear progression. What if the pattern is non-linear? We could explore:
- Polynomial sequences: These involve higher-order relationships between numbers. A simple quadratic or cubic equation could generate a sequence starting with 14, 15, 16, and 17, but the next number (x) would be determined by the specific equation used. There are countless polynomial functions that could fit these first four points.
- Recursive sequences: The value of x might depend on previous terms in a more complex manner. A recursive formula might define x as a function of 14, 15, 16, and 17, leading to a vastly different result.
3. A Sequence with a Modular Arithmetic Pattern:
Modular arithmetic involves working with remainders after division. For instance, consider the sequence modulo 5:
14 mod 5 = 4 15 mod 5 = 0 16 mod 5 = 1 17 mod 5 = 2
This suggests a pattern where the remainders are increasing by one each time. Following this logic, the next number (x) would have a remainder of 3 when divided by 5. Several numbers could fit this criterion: 18, 23, 28, and so on.
The Importance of Context: The Missing Piece of the Puzzle
The key takeaway is that determining the value of x hinges entirely on the context in which the sequence is presented. Without further information or clues, assigning a definitive value to x becomes impossible. The apparent simplicity of the question masks the deeper mathematical and logical complexities involved.
Expanding the Scope: Applications of Sequence Analysis
The principles involved in analyzing sequences like this have far-reaching applications across various fields:
1. Data Analysis and Forecasting: Identifying patterns in data is fundamental to forecasting trends, predicting future events, and making informed decisions. Techniques for analyzing numerical sequences are crucial tools in fields like finance, economics, and meteorology.
2. Cryptography and Coding: Sequences and patterns play a critical role in cryptography. Understanding how to create and decipher sequences helps secure information and protect sensitive data.
3. Computer Science and Algorithms: Algorithms often involve iterative processes that rely on numerical sequences. The study of sequences informs the design of efficient and effective algorithms.
4. Bioinformatics and Genomics: Identifying patterns in biological data, such as DNA sequences, is essential for understanding biological processes and developing new therapies.
Beyond Numbers: The Broader Implications of Problem-Solving
This seemingly simple number sequence problem illustrates broader principles of problem-solving:
- The importance of questioning assumptions: We must actively challenge our initial assumptions and consider alternative perspectives. The obvious solution might not always be the correct one.
- The need for context: Understanding the context of a problem is paramount in finding its solution. Without sufficient information, the question remains ill-defined.
- The value of multiple interpretations: Mathematics often allows for multiple solutions, depending on the interpretation and constraints imposed. Exploring these alternative solutions broadens our understanding.
- The iterative nature of problem-solving: Problem-solving is rarely a linear process. We often iterate through different approaches, refining our understanding as we go.
In conclusion, while the most likely answer to "What is the value of x in the sequence 14, 15, 16, 17?" is 18 based on a simple arithmetic progression, this seemingly basic question invites a deep exploration of mathematical thinking, problem-solving strategies, and the crucial role of context. The true value of the exercise lies not solely in finding the answer but in the process of questioning, analyzing, and appreciating the multifaceted nature of seemingly simple mathematical problems. It emphasizes the importance of critical thinking and the limitations of making assumptions in the quest for solutions. The journey to understanding the problem is often more valuable than the destination itself.
Latest Posts
Latest Posts
-
What Day Of The Week Is October 29th
May 23, 2025
-
60 Dollars With 30 Percent Off
May 23, 2025
-
What Percent Is 10 Out Of 16
May 23, 2025
-
6 Divided By 1 4 As A Fraction
May 23, 2025
-
What Is 2 3 Of 14
May 23, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of X 14 15 16 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.