What Is 2 3 Of 14
listenit
May 23, 2025 · 5 min read
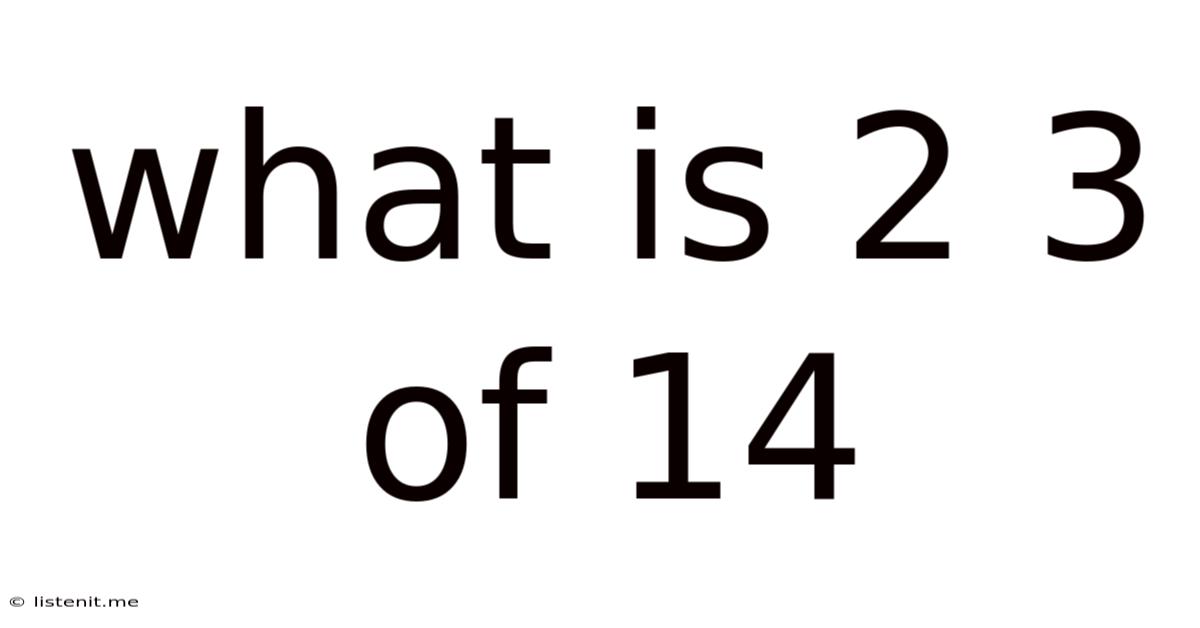
Table of Contents
What is 2/3 of 14? A Comprehensive Guide to Fractions and Their Applications
This seemingly simple question, "What is 2/3 of 14?", opens the door to a broader understanding of fractions, their practical applications, and how to solve them efficiently. While the answer itself is straightforward, the process of arriving at it, and the various contexts in which such calculations are used, offer valuable insights into mathematical concepts and real-world problem-solving. This article will delve deep into the subject, exploring different approaches, highlighting the importance of fractions, and providing examples to solidify your understanding.
Understanding Fractions: A Foundation for Calculation
Before tackling the specific problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
In our question, "What is 2/3 of 14?", 2 is the numerator and 3 is the denominator. This means we're interested in finding two out of three equal parts of 14.
Method 1: Converting to Decimal
One common approach is to convert the fraction into a decimal and then multiply. To convert 2/3 to a decimal, we divide the numerator (2) by the denominator (3):
2 ÷ 3 ≈ 0.6667 (This is an approximation, as 2/3 is a recurring decimal)
Now, multiply the decimal equivalent by 14:
0.6667 x 14 ≈ 9.3338
This method provides a quick approximate answer. However, it's important to remember that using the decimal approximation introduces a small degree of error, especially when dealing with complex calculations or situations requiring high precision.
Method 2: Multiplication of Fractions
A more accurate and conceptually clearer method involves directly multiplying the fraction by the whole number. To do this, we first need to express 14 as a fraction: 14/1. Then, we multiply the two fractions:
(2/3) x (14/1) = (2 x 14) / (3 x 1) = 28/3
Now, we have an improper fraction (where the numerator is larger than the denominator). To express this as a mixed number (a whole number and a fraction), we divide the numerator (28) by the denominator (3):
28 ÷ 3 = 9 with a remainder of 1
This means that 28/3 is equal to 9 and 1/3. Therefore, 2/3 of 14 is 9 1/3. This method provides the exact answer without the rounding errors associated with decimal approximations.
Method 3: Breaking Down the Problem
Another approach involves dividing the whole number by the denominator and then multiplying by the numerator. This method is intuitively helpful for visualizing the problem:
-
Divide: Divide 14 by the denominator (3): 14 ÷ 3 ≈ 4.6667. This represents the size of one-third of 14.
-
Multiply: Multiply the result by the numerator (2): 4.6667 x 2 ≈ 9.3334. This represents two-thirds of 14.
Again, this method involves a decimal approximation, leading to a slight inaccuracy. However, it provides a step-by-step approach that can be more easily grasped.
Real-World Applications: Where Fractions Matter
The seemingly simple calculation of "2/3 of 14" has numerous real-world applications across diverse fields:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. For instance, a recipe might require 2/3 cup of sugar. Knowing how to calculate fractions is essential for accurately measuring ingredients and achieving the desired results.
-
Construction and Engineering: Precision is paramount in construction and engineering projects. Fractions are used extensively in measurements, calculations of materials needed, and ensuring structural integrity.
-
Finance and Economics: Understanding fractions is crucial for calculating interest rates, discounts, percentages, and other financial concepts. For example, determining a 2/3 discount on an item requires fractional calculations.
-
Data Analysis and Statistics: Data is often represented and analyzed using fractions and percentages, providing insights and conclusions. Understanding these representations is vital for interpreting data effectively.
-
Everyday Life: From dividing a pizza among friends to calculating portions for a shared meal, fractions are integral to our daily lives.
Advanced Concepts Related to Fractions
Understanding "2/3 of 14" opens the door to more advanced concepts, including:
-
Equivalent Fractions: Fractions can be expressed in different forms while maintaining the same value. For example, 2/3 is equivalent to 4/6, 6/9, and so on. Understanding equivalent fractions is helpful for simplifying calculations and finding common denominators.
-
Improper and Mixed Fractions: As seen in our calculation, an improper fraction has a numerator larger than the denominator (e.g., 28/3), while a mixed fraction combines a whole number and a fraction (e.g., 9 1/3). Knowing how to convert between these forms is crucial for various mathematical operations.
-
Operations with Fractions: Beyond simple multiplication, understanding how to add, subtract, and divide fractions is essential for solving more complex problems.
Practical Tips and Strategies for Mastering Fractions
-
Practice Regularly: The more you practice working with fractions, the more comfortable and proficient you will become.
-
Visual Aids: Utilize visual aids like diagrams or pie charts to visualize fractions and their relationships.
-
Break Down Complex Problems: Break down complex problems into smaller, more manageable steps.
-
Utilize Online Resources: Many online resources, including calculators and tutorials, can assist you in learning and practicing fractions.
-
Seek Help When Needed: Don't hesitate to seek help from teachers, tutors, or online communities if you're struggling with a particular concept.
Conclusion: Beyond the Answer
While the answer to "What is 2/3 of 14?" is 9 1/3, the true value lies in understanding the underlying principles of fractions, their diverse applications, and the various methods for solving such problems. Mastering fractions is not just about arriving at a numerical answer but also about developing critical thinking skills, problem-solving abilities, and a deeper appreciation for the foundational concepts of mathematics. This understanding extends beyond the classroom and plays a vital role in navigating many aspects of daily life and professional endeavors. By embracing the learning process and dedicating time to practice, you'll not only solve this specific problem but also develop a strong foundation in fractions that will serve you well in many future endeavors.
Latest Posts
Latest Posts
-
Business Line Of Credit Payment Calculator
May 24, 2025
-
Write The Number 280 In Scientific Notation
May 24, 2025
-
How Much Is A Mortgage On A 150k House
May 24, 2025
-
Greatest Common Factor Of 28 And 44
May 24, 2025
-
What Is 3 4 X 1 2
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Of 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.