What Is The Square Root Of One Fourth
listenit
Apr 03, 2025 · 5 min read
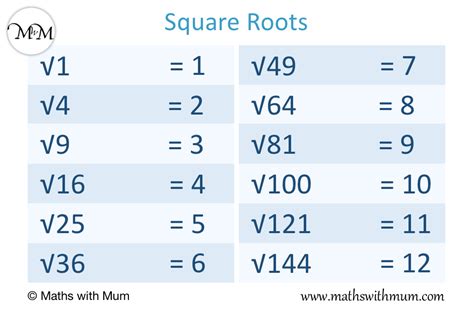
Table of Contents
What is the Square Root of One Fourth? A Deep Dive into Square Roots and Fractions
The question, "What is the square root of one fourth?" might seem deceptively simple. However, understanding its answer unlocks a deeper appreciation of square roots, fractions, and their interplay within mathematics. This comprehensive guide will not only answer this question but also explore the underlying mathematical concepts, providing a solid foundation for more advanced mathematical explorations.
Understanding Square Roots
Before tackling the square root of one-fourth, let's solidify our understanding of square roots in general. The square root of a number is a value that, when multiplied by itself, equals the original number. For instance, the square root of 9 is 3 because 3 multiplied by itself (3 x 3 = 9) equals 9. We denote the square root using the radical symbol (√). So, √9 = 3.
It's crucial to remember that every positive number has two square roots: a positive and a negative one. For example, while 3 is a square root of 9, so is -3 because (-3) x (-3) = 9. However, when we write √9, we typically refer to the principal square root, which is the positive square root (3 in this case). This convention is important to avoid ambiguity.
Exploring Different Types of Square Roots
We encounter various types of square roots:
-
Perfect Squares: These are numbers that have whole number square roots. Examples include 4 (√4 = 2), 25 (√25 = 5), and 100 (√100 = 10).
-
Non-Perfect Squares: These numbers do not have whole number square roots. Examples include 2 (√2 ≈ 1.414), 7 (√7 ≈ 2.646), and 15 (√15 ≈ 3.873). Their square roots are irrational numbers, meaning they cannot be expressed as a simple fraction.
-
Square Roots of Fractions: These involve finding the square root of a fractional number. This is where our main focus lies, as it's directly related to the question at hand.
-
Square Roots of Negative Numbers: These are imaginary numbers, denoted by the imaginary unit 'i', where i² = -1. This is a fascinating area of mathematics but lies outside the scope of our current discussion.
Tackling the Square Root of One-Fourth
Now, let's address the core question: What is the square root of one-fourth (√(1/4))?
There are two primary approaches to solving this:
Method 1: Applying the Square Root to the Numerator and Denominator
This method leverages the property that the square root of a fraction is equal to the square root of the numerator divided by the square root of the denominator. Therefore:
√(1/4) = √1 / √4
Since √1 = 1 and √4 = 2, we get:
√(1/4) = 1/2
Therefore, the square root of one-fourth is one-half (1/2).
Method 2: Converting the Fraction to a Decimal
We can also solve this by first converting the fraction 1/4 into its decimal equivalent (0.25). Then, we calculate the square root of the decimal:
√(1/4) = √0.25 = 0.5
Since 0.5 is equivalent to 1/2, we arrive at the same answer: the square root of one-fourth is one-half (1/2).
Expanding Our Understanding: Square Roots and Fractions
Understanding the square root of one-fourth offers a springboard to explore the broader relationship between square roots and fractions.
Working with More Complex Fractions
Let's consider more complex examples:
-
√(9/25): Using the same principle, we calculate √9 / √25 = 3/5.
-
√(16/49): Similarly, √16 / √49 = 4/7.
-
√(25/100): This simplifies to √25 / √100 = 5/10 = 1/2. Note that this is equivalent to √(1/4), illustrating the versatility of simplifying fractions before calculating square roots.
Dealing with Non-Perfect Square Fractions
Not all fractions will yield whole number square roots. For instance, √(2/9) would result in √2 / √9 = √2 / 3. Here, we end up with an irrational number (√2) in the numerator. This highlights the fact that even with fractions, the outcome might be an irrational number.
The Importance of Simplification
Before calculating square roots, it's always beneficial to simplify the fraction to its lowest terms. This simplifies the calculation and often makes the square root easier to determine.
Practical Applications and Real-World Examples
The concept of square roots and fractions isn't limited to abstract mathematical exercises. It has numerous practical applications in various fields:
-
Geometry: Calculating the side lengths of squares and other geometric figures often involves dealing with square roots and fractions. For instance, finding the diagonal of a square with a side length of 1/2 requires understanding the concept of the square root of a fraction.
-
Physics: Many physics formulas involve square roots, particularly those related to motion, energy, and forces. These equations often use fractions to represent ratios and proportions, which can then necessitate the understanding of square roots of fractions.
-
Engineering: In structural engineering and other engineering disciplines, calculations involving dimensions and stresses frequently require working with square roots of fractions.
-
Computer Graphics and Game Development: Precise rendering of objects in 2D and 3D space involves frequent use of square roots to scale and reposition objects according to their coordinates. This process may involve fractions and decimal values, thus combining different aspects of square root calculation.
-
Finance: Compound interest calculations in finance often involve square roots, particularly when solving for the time required for an investment to reach a certain value. This would often be related to various fractional values representing the interest rate.
Conclusion: Mastering Square Roots and Fractions
The seemingly simple question, "What is the square root of one-fourth?" opens the door to a rich understanding of square roots, fractions, and their interrelationship within mathematics and its applications. Mastering these concepts provides a crucial building block for further mathematical exploration and problem-solving in various fields. By understanding the principles outlined here, and through consistent practice, you'll solidify your grasp on these vital mathematical tools, preparing you for more complex mathematical challenges. The ability to work confidently with square roots of fractions is essential for success in many areas, making this a crucial skill to develop. Remember to always simplify your fractions before calculating the square root whenever possible, and you will find it easier to manage!
Latest Posts
Latest Posts
-
What Percentage Is 20 Out Of 50
Apr 04, 2025
-
How Does An Igneous Rock Turn Into A Metamorphic Rock
Apr 04, 2025
-
What Is The Lcm Of 6 And 5
Apr 04, 2025
-
Which One Increases Number Of Collisions Between The Reactants
Apr 04, 2025
-
How Many Feet In 1 2 Miles
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of One Fourth . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
