What Is The Square Root Of 784
listenit
Apr 01, 2025 · 5 min read
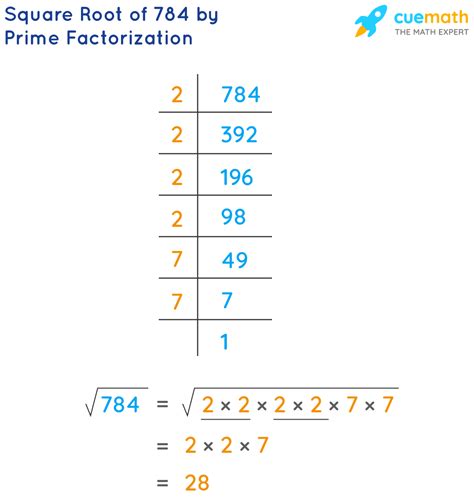
Table of Contents
What is the Square Root of 784? A Deep Dive into Square Roots and their Applications
Finding the square root of a number might seem like a simple mathematical operation, but understanding the process and its implications opens doors to a fascinating world of numbers and their properties. This article delves into the question, "What is the square root of 784?", exploring various methods to calculate it, its significance in mathematics, and its practical applications in diverse fields.
Understanding Square Roots
Before we tackle the square root of 784, let's solidify our understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9. Mathematically, we represent this as: √9 = 3.
The square root operation is the inverse of squaring a number. Squaring a number means multiplying it by itself. So, if we square 3 (3 x 3), we get 9. Finding the square root reverses this process, taking us from 9 back to 3.
Calculating the Square Root of 784: Different Approaches
There are several ways to calculate the square root of 784. Let's explore some common methods:
1. Prime Factorization Method
This method involves breaking down the number 784 into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, etc.).
-
Find the prime factors of 784: 784 = 2 x 392 = 2 x 2 x 196 = 2 x 2 x 2 x 98 = 2 x 2 x 2 x 2 x 49 = 2 x 2 x 2 x 2 x 7 x 7 = 2⁴ x 7²
-
Pair up the prime factors: We have four 2s and two 7s.
-
Take one factor from each pair: This gives us 2 x 2 x 7 = 28
Therefore, the square root of 784 is 28.
2. Using a Calculator
The simplest and fastest method is using a calculator. Most calculators have a square root function (√) that directly calculates the square root of a number. Simply enter 784 and press the square root button. The result will be 28.
3. Long Division Method
The long division method is a more manual approach, useful for understanding the underlying process. It's a bit more complex but provides a deeper insight into how square roots are calculated without relying on a calculator. While detailing the entire long division method here would be extensive, it's a readily available method that can be researched further. The result, as expected, is 28.
The Significance of the Square Root of 784
The number 28, as the square root of 784, holds significance in various mathematical contexts. Its relationship to 784 highlights the fundamental concepts of squares and square roots. Understanding this relationship is crucial for various mathematical calculations and problem-solving.
Practical Applications of Square Roots
Square roots are far from being a purely theoretical mathematical concept. They have wide-ranging applications in numerous fields:
1. Geometry and Measurement
Square roots are fundamental in geometry, particularly when dealing with areas and distances. For instance, calculating the length of the diagonal of a square or rectangle often involves finding the square root. If a square has an area of 784 square units, its side length would be the square root of 784, which is 28 units.
2. Physics and Engineering
In physics and engineering, square roots frequently appear in formulas related to motion, energy, and forces. Calculations involving velocity, acceleration, and energy often necessitate the use of square roots.
3. Statistics and Data Analysis
Square roots are essential in statistical analysis, particularly when dealing with standard deviations and variances. Standard deviation, a crucial measure of data dispersion, involves calculating the square root of the variance.
4. Computer Graphics and Game Development
In computer graphics and game development, square roots are crucial for calculating distances between points in 2D and 3D spaces. This is fundamental for collision detection, pathfinding, and rendering realistic scenes.
5. Finance and Investment
Square roots are used in financial modeling and risk assessment. Calculations involving portfolio variance and standard deviation rely heavily on the square root operation.
Beyond the Basics: Exploring Higher-Order Roots
While we have focused on square roots, it's important to note that higher-order roots exist. A cube root (∛) finds a number that, when multiplied by itself three times, gives the original number. Similarly, fourth roots, fifth roots, and so on, are defined in analogous ways.
Understanding square roots forms a strong foundation for comprehending these higher-order root concepts.
Perfect Squares and their Importance
The number 784 is a perfect square because it is the square of a whole number (28). Perfect squares are numbers that can be obtained by squaring an integer. Identifying perfect squares is often helpful in simplifying mathematical expressions and solving equations.
Solving Equations Involving Square Roots
Many equations involve square roots. Consider the equation x² = 784. To solve for x, we take the square root of both sides, resulting in x = ±28 (positive and negative 28, since both (-28)² and (28)² equal 784). This demonstrates the importance of square roots in solving algebraic equations.
Approximating Square Roots
While we've focused on finding the exact square root of 784, it's useful to know how to approximate square roots for numbers that aren't perfect squares. Approximation methods, such as using iterative techniques or employing Taylor series expansions, can be used to obtain reasonably accurate estimates.
Conclusion: The Ubiquity of Square Roots
The square root of 784, which is 28, represents a simple yet fundamental concept in mathematics with far-reaching consequences. From the simple geometry of a square to the complex calculations of quantum physics, understanding square roots is essential for navigating a broad range of fields. This article has explored various methods for calculating square roots and highlighted their widespread applications. As you delve deeper into mathematics and its related disciplines, you'll continue to encounter the significance and practicality of square roots. The seemingly simple question "What is the square root of 784?" opens doors to a wealth of mathematical understanding and practical applications. Remember to practice different methods to solidify your grasp of this crucial mathematical operation.
Latest Posts
Latest Posts
-
Lowest Common Multiple Of 32 And 48
Apr 02, 2025
-
What Is The Greatest Common Factor Of 8 And 24
Apr 02, 2025
-
A Solution In Which The Solvent Is Water
Apr 02, 2025
-
Is Air A Compound Or An Element
Apr 02, 2025
-
How Many Electrons Are In Mercury
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 784 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
