What Is The Square Root Of 67
listenit
Apr 04, 2025 · 5 min read
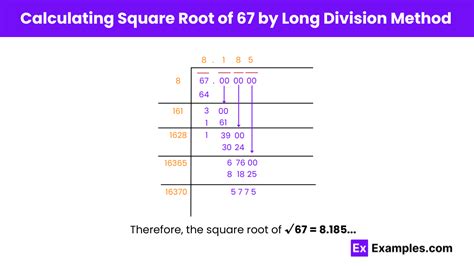
Table of Contents
What is the Square Root of 67? A Deep Dive into Irrational Numbers and Approximation Techniques
The seemingly simple question, "What is the square root of 67?" opens a fascinating door into the world of mathematics, specifically the realm of irrational numbers and numerical approximation techniques. While a precise, finite decimal representation of √67 is impossible, we can explore various methods to find increasingly accurate approximations. This article will delve into the nature of irrational numbers, explore different methods for approximating √67, and discuss their applications in various fields.
Understanding Irrational Numbers
Before we delve into the approximation techniques, let's establish the fundamental nature of √67. The square root of a number 'x' is a value that, when multiplied by itself, equals x. In simpler terms, it's the number that, when squared, gives you the original number. For example, the square root of 9 is 3 because 3 x 3 = 9.
However, not all numbers have perfect square roots. Numbers like 67 are not perfect squares; there is no integer that, when multiplied by itself, equals 67. Such numbers possess square roots that are irrational numbers. Irrational numbers are numbers that cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representations are non-terminating and non-repeating – they go on forever without ever settling into a repeating pattern. This is why we can only approximate √67, not express it exactly.
Methods for Approximating √67
Several methods exist to approximate the square root of 67 to varying degrees of accuracy. Let's explore some of the most common and effective techniques:
1. Babylonian Method (Heron's Method)
The Babylonian method, also known as Heron's method, is an iterative algorithm that refines an initial guess to progressively closer approximations. It's based on the principle that if 'x' is an overestimate of √67, then 67/x will be an underestimate, and the average of these two values will be a better approximation.
The steps are:
- Make an initial guess: Let's start with a guess of 8 (since 8² = 64, which is close to 67).
- Iterate: Use the formula: x_(n+1) = 0.5 * (x_n + 67/x_n), where x_n is the current approximation and x_(n+1) is the next approximation.
- Repeat: Repeat step 2 until the desired level of accuracy is achieved.
Let's perform a few iterations:
- Iteration 1: x_1 = 0.5 * (8 + 67/8) ≈ 8.25
- Iteration 2: x_2 = 0.5 * (8.25 + 67/8.25) ≈ 8.182
- Iteration 3: x_3 = 0.5 * (8.182 + 67/8.182) ≈ 8.185
As you can see, the approximation quickly converges to a value close to the actual square root. With each iteration, the accuracy improves.
2. Newton-Raphson Method
The Newton-Raphson method is another iterative technique for finding successively better approximations to the roots of a real-valued function. Applied to finding √67, we consider the function f(x) = x² - 67. The square root of 67 is the root of this function (where f(x) = 0).
The formula for the Newton-Raphson method is: x_(n+1) = x_n - f(x_n) / f'(x_n), where f'(x) is the derivative of f(x). In our case, f'(x) = 2x.
Starting with an initial guess (let's again use 8), we can iterate:
- Iteration 1: x_1 = 8 - (8² - 67) / (2 * 8) ≈ 8.1875
- Iteration 2: x_2 = 8.1875 - (8.1875² - 67) / (2 * 8.1875) ≈ 8.18535
Again, this method rapidly converges towards the actual value.
3. Using a Calculator or Computer Software
Modern calculators and computer software packages provide built-in functions for calculating square roots to a high degree of precision. These typically employ sophisticated algorithms, often variations or improvements on the methods discussed above, to achieve very accurate approximations. Using a calculator, we find that √67 ≈ 8.18535277187...
Applications of Square Roots and Approximation Techniques
The ability to calculate or approximate square roots is fundamental to various fields:
-
Physics and Engineering: Square roots are ubiquitous in physics and engineering calculations. For example, calculating velocities, distances, or forces often involves square roots. Accurate approximations are crucial for designing structures, predicting trajectories, or understanding physical phenomena.
-
Geometry and Trigonometry: The Pythagorean theorem, a cornerstone of geometry, directly involves square roots. Calculating distances, areas, or volumes in various geometric shapes relies heavily on this theorem and thus on square root calculations. Trigonometry also utilizes square roots in numerous formulas.
-
Computer Graphics and Game Development: Rendering 3D graphics, simulating physical effects in games, and calculating lighting and shadows all utilize square root computations. Efficient approximation techniques are essential for real-time performance in these applications.
-
Finance and Statistics: Financial models frequently incorporate square roots, particularly in calculations related to standard deviation, variance, and risk assessment. Accurate estimations are necessary for making informed financial decisions.
-
Computer Science: Many algorithms in computer science rely on square root calculations for optimization or efficiency. Understanding approximation methods is crucial for developing fast and robust algorithms.
Conclusion
While the square root of 67 is an irrational number and lacks a precise, finite decimal representation, various methods allow us to approximate it to any desired degree of accuracy. The Babylonian method, Newton-Raphson method, and built-in functions in calculators and software provide effective tools for this purpose. The ability to efficiently approximate square roots is crucial for a wide range of applications across multiple disciplines, underscoring its importance in both theoretical and practical contexts. The seemingly simple question of "What is the square root of 67?" opens up a fascinating exploration into the world of mathematics and its real-world impact. The continuous refinement of approximation methods reflects the ongoing pursuit of precision and efficiency in computation.
Latest Posts
Latest Posts
-
Two Thirds Of A Number Algebraic Expression
Apr 04, 2025
-
Is Photosynthesis A Chemical Or Physical Change
Apr 04, 2025
-
Convert 101 Degrees Fahrenheit To Celsius
Apr 04, 2025
-
How Many Minute In A Week
Apr 04, 2025
-
How Do Humans Impact Phosphorus Cycle
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 67 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
