What Is The Square Root Of 2 Squared
listenit
Mar 27, 2025 · 5 min read
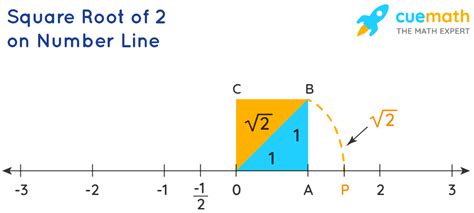
Table of Contents
What is the Square Root of 2 Squared? A Deep Dive into Mathematical Fundamentals
The seemingly simple question, "What is the square root of 2 squared?" opens a door to a fascinating exploration of fundamental mathematical concepts. While the answer might seem immediately obvious, a deeper dive reveals intricate connections between exponents, roots, and the very nature of numbers. This article will not only answer the question directly but will also delve into the underlying mathematical principles, providing a comprehensive understanding for both beginners and those seeking a more rigorous exploration.
Understanding Squares and Square Roots
Before tackling the core question, let's establish a solid foundation. A square of a number is the result of multiplying that number by itself. For example, the square of 3 (written as 3²) is 3 * 3 = 9. Similarly, the square of 2 (2²) is 2 * 2 = 4.
The square root, conversely, is the inverse operation. It's the number that, when multiplied by itself, yields the original number. For instance, the square root of 9 (written as √9) is 3, because 3 * 3 = 9. The square root of 4 (√4) is 2, because 2 * 2 = 4.
Answering the Question: √(2²)
Now, let's address the main question: What is the square root of 2 squared? Mathematically, this is represented as √(2²).
Following the order of operations (PEMDAS/BODMAS), we first calculate the square of 2: 2² = 4.
Then, we find the square root of the result: √4 = 2.
Therefore, the square root of 2 squared is 2.
Beyond the Simple Answer: Exploring the Concepts
While the answer itself is straightforward, the underlying mathematical principles are rich and multifaceted. Let's explore some of these concepts:
The Relationship Between Squaring and Square Rooting
Squaring and square rooting are inverse operations. This means they essentially "undo" each other. Just as addition and subtraction are inverses, and multiplication and division are inverses, squaring and square rooting are inverses. This inverse relationship is crucial in understanding the simplicity of the solution to our original question.
The Concept of Principal Square Roots
It's important to note the concept of the principal square root. While (-2) * (-2) also equals 4, the principal square root of 4 is conventionally defined as 2 (the positive root). This convention is essential for consistency and avoids ambiguity in mathematical calculations.
Extending the Concept to Other Numbers
The relationship between squaring and square rooting holds true for other numbers as well. For any non-negative real number 'x', the square root of x squared is always x: √(x²) = x. This is a fundamental property within the realm of real numbers.
Dealing with Negative Numbers
When dealing with negative numbers, things get slightly more complex. The square of a negative number is always positive. For example, (-2)² = 4. However, the square root of a number is defined only for non-negative numbers within the context of real numbers. To deal with the square roots of negative numbers, we need to introduce the concept of imaginary numbers, which involves the imaginary unit 'i', where i² = -1.
Applications in Various Fields
The concept of squares and square roots extends far beyond basic arithmetic. They are fundamental components in various fields, including:
- Physics: Calculating distances, velocities, and accelerations.
- Engineering: Designing structures, analyzing forces, and solving equations.
- Computer Science: Developing algorithms, working with data structures, and solving computational problems.
- Finance: Calculating compound interest, risk management, and portfolio optimization.
- Geometry: Finding the lengths of sides and diagonals in shapes and solving geometric problems involving right triangles and the Pythagorean theorem.
The Pythagorean Theorem: A Key Application
One of the most significant applications of squares and square roots lies within the Pythagorean Theorem. This theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (the legs).
The formula is expressed as: a² + b² = c², where 'a' and 'b' are the lengths of the legs, and 'c' is the length of the hypotenuse. Solving for the length of one side often requires using square roots. For instance, if you know 'a' and 'b', you can find 'c' using the square root of (a² + b²).
Advanced Concepts and Extensions
The exploration of squares and square roots can extend to more advanced mathematical concepts:
- Higher-order roots: Cube roots, fourth roots, and beyond. These are generalizations of the square root concept. The nth root of a number 'x' is a number that, when multiplied by itself 'n' times, equals 'x'.
- Complex numbers: As mentioned earlier, the square root of negative numbers involves imaginary numbers and leads to the broader concept of complex numbers, which extend the number system beyond real numbers.
- Irrational numbers: The square root of 2 (√2) is an example of an irrational number, meaning it cannot be expressed as a simple fraction. This number has an infinite non-repeating decimal representation.
Conclusion: A Foundation for Deeper Understanding
The seemingly trivial question of "What is the square root of 2 squared?" serves as a springboard for exploring profound mathematical concepts. From the inverse relationship between squaring and square rooting to the applications in various fields and the expansion into more complex number systems, the journey from this simple question reveals the rich tapestry of mathematical theory. Understanding these foundational concepts builds a solid base for further exploration in mathematics and related disciplines. The simplicity of the answer – 2 – belies the depth of the mathematical ideas it represents. The exploration helps foster a deeper appreciation for the elegance and power of mathematics.
Latest Posts
Latest Posts
-
What Is The Percentage Of 12 Out Of 15
Mar 30, 2025
-
What Is The Gcf Of 25 And 15
Mar 30, 2025
-
60 Is What Percent Of 40
Mar 30, 2025
-
What Do The Coefficients In A Chemical Equation Represent
Mar 30, 2025
-
Is Table Salt A Heterogeneous Mixture
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 2 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
