What Is The Slope Of The Line Shown Below
listenit
Mar 30, 2025 · 5 min read
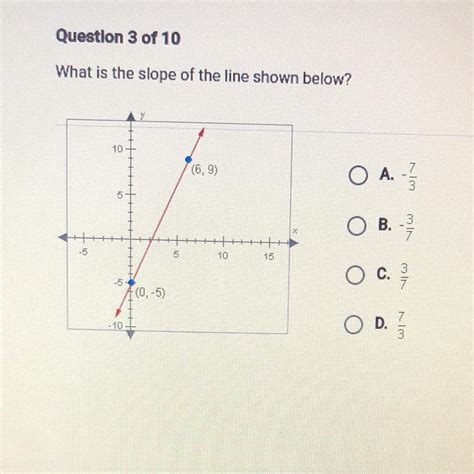
Table of Contents
What is the Slope of the Line Shown Below? A Comprehensive Guide
Understanding the slope of a line is fundamental in algebra and geometry, forming the bedrock for numerous applications in various fields, from physics and engineering to economics and data science. This comprehensive guide will delve deep into determining the slope of a line, exploring different methods, tackling various scenarios, and providing practical examples to solidify your understanding. We will cover everything from basic definitions to more advanced concepts, ensuring you grasp the concept thoroughly.
Defining the Slope
The slope of a line is a measure of its steepness. It quantifies how much the y-value changes for every unit change in the x-value. Mathematically, the slope (often represented by the letter 'm') is defined as the ratio of the vertical change (rise) to the horizontal change (run) between any two distinct points on the line.
Formula:
The most common formula for calculating the slope is:
m = (y₂ - y₁) / (x₂ - x₁)
where (x₁, y₁) and (x₂, y₂) are the coordinates of any two points on the line.
Key Considerations:
- Positive Slope: A positive slope indicates that the line is increasing (going uphill from left to right).
- Negative Slope: A negative slope indicates that the line is decreasing (going downhill from left to right).
- Zero Slope: A zero slope indicates that the line is horizontal (parallel to the x-axis).
- Undefined Slope: An undefined slope indicates that the line is vertical (parallel to the y-axis). This occurs when the denominator (x₂ - x₁) is equal to zero.
Methods for Determining the Slope
Let's explore different methods for determining the slope of a line, depending on the information provided:
1. Using Two Points
This is the most common method. If you have the coordinates of two points on the line, you can directly apply the slope formula:
Example:
Find the slope of the line passing through points A(2, 4) and B(6, 10).
- Identify the coordinates: (x₁, y₁) = (2, 4) and (x₂, y₂) = (6, 10)
- Apply the formula: m = (10 - 4) / (6 - 2) = 6 / 4 = 3/2
Therefore, the slope of the line is 3/2. This indicates a positive slope, meaning the line increases as x increases.
2. Using the Equation of the Line
The equation of a line is often expressed in slope-intercept form:
y = mx + b
where 'm' is the slope and 'b' is the y-intercept (the point where the line crosses the y-axis).
Example:
Find the slope of the line represented by the equation y = 2x + 5.
The equation is already in slope-intercept form. By comparing it to y = mx + b, we can directly identify the slope: m = 2.
3. Using a Graph
If you have a graph of the line, you can determine the slope by selecting two points on the line and calculating the rise and run.
Steps:
- Choose two points: Select any two distinct points on the line.
- Calculate the rise: Find the vertical distance (difference in y-coordinates) between the two points.
- Calculate the run: Find the horizontal distance (difference in x-coordinates) between the two points.
- Calculate the slope: Divide the rise by the run.
Example (Graphical Illustration Needed Here - Imagine a line on a graph):
Let's say you select points (1, 2) and (4, 5).
- Rise = 5 - 2 = 3
- Run = 4 - 1 = 3
- Slope = Rise / Run = 3 / 3 = 1
Advanced Concepts and Special Cases
Parallel and Perpendicular Lines
- Parallel Lines: Parallel lines have the same slope. If two lines are parallel, they will never intersect.
- Perpendicular Lines: Perpendicular lines have slopes that are negative reciprocals of each other. If the slope of one line is 'm', the slope of a line perpendicular to it is '-1/m'.
Lines with Undefined Slope
As mentioned earlier, vertical lines have an undefined slope. This is because the change in x (run) is always zero, resulting in division by zero, which is undefined in mathematics.
Lines with Zero Slope
Horizontal lines have a slope of zero. This is because the change in y (rise) is always zero.
Applications of Slope
The concept of slope has widespread applications across various fields:
- Physics: Calculating velocity, acceleration, and the gradient of a curve.
- Engineering: Determining the angle of inclination in construction and design.
- Economics: Analyzing the relationship between variables like price and demand.
- Data Science: Creating linear regression models to predict future outcomes.
- Computer Graphics: Defining the orientation and direction of lines and objects.
Troubleshooting Common Mistakes
- Incorrectly identifying points: Double-check the coordinates of the points you are using.
- Reversing the order of subtraction: Remember to maintain consistency when subtracting the x and y coordinates.
- Misinterpreting the sign of the slope: A negative slope indicates a decreasing line, while a positive slope indicates an increasing line.
- Forgetting about vertical and horizontal lines: Remember that vertical lines have undefined slopes and horizontal lines have zero slopes.
Conclusion
Understanding the slope of a line is crucial for many areas of mathematics and its applications. This guide has provided a comprehensive overview, covering various methods for calculating slope and highlighting important considerations. By mastering this fundamental concept, you'll build a strong foundation for more advanced mathematical concepts and their real-world applications. Remember to practice regularly to solidify your understanding and build confidence in tackling various slope-related problems. The more you practice, the easier it will become to quickly and accurately determine the slope of any line.
Latest Posts
Latest Posts
-
How Long Is 1 4 Of A Mile
Apr 01, 2025
-
What Percent Of 35 Is 14
Apr 01, 2025
-
What Is The Square Root Of 784
Apr 01, 2025
-
What Is Conjugate Base Of Hso4
Apr 01, 2025
-
What Are The Three Parts Of Atp
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Slope Of The Line Shown Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
