What Is The Length Of In The Right Triangle Below
listenit
Mar 30, 2025 · 5 min read
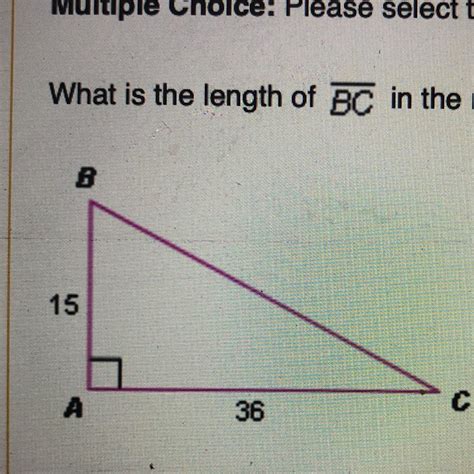
Table of Contents
Decoding the Right Triangle: Determining Leg Lengths and Hypotenuse
Understanding right triangles is fundamental in various fields, from basic geometry to advanced physics and engineering. A right triangle, by definition, contains one 90-degree angle (a right angle). This unique characteristic allows us to utilize the Pythagorean theorem and trigonometric functions to solve for unknown sides and angles. This article delves into the intricacies of calculating the length of sides in a right-angled triangle, focusing on practical applications and problem-solving techniques. We'll explore different scenarios, employing both the Pythagorean theorem and trigonometric ratios (sine, cosine, and tangent) to illustrate how to determine the length of any side, given sufficient information.
The Pythagorean Theorem: The Cornerstone of Right Triangle Calculations
The Pythagorean theorem is arguably the most important concept when dealing with right triangles. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (called legs or cathetus). Mathematically, this is represented as:
a² + b² = c²
Where:
- a and b represent the lengths of the two legs.
- c represents the length of the hypotenuse.
This theorem allows us to calculate the length of any unknown side if we know the lengths of the other two. Let's illustrate this with some examples:
Example 1: Finding the Hypotenuse
Suppose we have a right triangle with legs of length a = 3 units and b = 4 units. To find the length of the hypotenuse (c), we apply the Pythagorean theorem:
3² + 4² = c²
9 + 16 = c²
25 = c²
c = √25 = 5 units
Therefore, the length of the hypotenuse is 5 units.
Example 2: Finding a Leg Length
Let's consider a right triangle with a hypotenuse of length c = 10 units and one leg of length a = 6 units. We want to find the length of the other leg (b). We rearrange the Pythagorean theorem:
a² + b² = c²
b² = c² - a²
b² = 10² - 6²
b² = 100 - 36
b² = 64
b = √64 = 8 units
Thus, the length of the missing leg is 8 units.
Beyond the Pythagorean Theorem: Introducing Trigonometric Functions
While the Pythagorean theorem is crucial for finding side lengths when two sides are known, trigonometric functions become essential when dealing with angles and one side. The three primary trigonometric functions are:
- Sine (sin): sin(θ) = opposite/hypotenuse
- Cosine (cos): cos(θ) = adjacent/hypotenuse
- Tangent (tan): tan(θ) = opposite/adjacent
Where θ represents the angle we are considering. "Opposite" refers to the side opposite the angle, and "adjacent" refers to the side next to the angle (excluding the hypotenuse).
Example 3: Using Sine to Find a Side Length
Imagine a right triangle with a hypotenuse of length c = 12 units and an angle θ = 30 degrees. We want to find the length of the side opposite to this angle (let's call it 'a'). We use the sine function:
sin(30°) = a/12
a = 12 * sin(30°)
Since sin(30°) = 0.5,
a = 12 * 0.5 = 6 units
Therefore, the length of the opposite side is 6 units.
Example 4: Using Cosine to Find a Side Length
Consider a right triangle with a hypotenuse of length c = 15 units and an angle θ = 45 degrees. We need to find the length of the side adjacent to this angle (let's call it 'b'). We use the cosine function:
cos(45°) = b/15
b = 15 * cos(45°)
Since cos(45°) ≈ 0.707,
b ≈ 15 * 0.707 ≈ 10.6 units
Therefore, the length of the adjacent side is approximately 10.6 units.
Example 5: Using Tangent to Find a Side Length
Suppose we have a right triangle with one leg (a) of length 5 units and an angle θ = 60 degrees. We want to find the length of the other leg (b) which is opposite the given angle. We use the tangent function:
tan(60°) = b/5
b = 5 * tan(60°)
Since tan(60°) ≈ 1.732,
b ≈ 5 * 1.732 ≈ 8.66 units
Therefore, the length of the opposite side is approximately 8.66 units.
Solving Right Triangles: A Comprehensive Approach
Solving a right triangle means finding the lengths of all its sides and the measures of all its angles. This often involves a combination of the Pythagorean theorem and trigonometric functions. The strategy depends on the information given:
- If two sides are known: Use the Pythagorean theorem to find the third side.
- If one side and one angle (other than the right angle) are known: Use trigonometric functions to find the other sides.
- If two angles are known: Since the sum of angles in a triangle is 180 degrees, and one angle is 90 degrees, the third angle can be easily calculated. Then, use trigonometric functions to find the side lengths.
It's important to note that accurate calculations often require a calculator with trigonometric functions. Rounding errors can accumulate if calculations are performed manually.
Practical Applications of Right Triangle Calculations
The ability to calculate side lengths in right triangles is crucial in numerous practical applications:
- Construction and Engineering: Determining the height of buildings, calculating distances for infrastructure projects, and designing ramps and slopes.
- Navigation: Calculating distances and bearings in surveying and GPS technology.
- Physics and Engineering: Analyzing projectile motion, resolving forces into components, and solving problems related to vectors.
- Computer Graphics and Game Development: Creating realistic 3D models and simulations.
- Surveying and Land Measurement: Determining land boundaries and areas.
Advanced Concepts and Considerations
While the basics are covered above, more advanced concepts exist for solving complex scenarios:
- Law of Sines and Law of Cosines: These laws extend the capabilities beyond right triangles to solve any triangle, regardless of its angles.
- Vectors and Vector Resolution: Representing forces and other physical quantities as vectors often necessitates the use of right-angled triangles for resolution.
- Calculus and Related Rates: In calculus, the concept of the right triangle is often applied to problems involving rates of change and derivatives.
Conclusion
Understanding how to determine the length of sides in a right triangle is a fundamental skill with widespread applications. The Pythagorean theorem and trigonometric functions provide powerful tools for solving a variety of problems. Mastering these techniques is crucial for success in various fields, from mathematics and engineering to computer science and beyond. Remember that consistent practice and a thorough understanding of the concepts are key to effectively applying these principles. By combining the theoretical knowledge with practical exercises, you can build a strong foundation in right-triangle geometry and unlock its numerous applications.
Latest Posts
Latest Posts
-
3 As A Percentage Of 8
Apr 01, 2025
-
What Is 20 Off Of 600
Apr 01, 2025
-
Why Is Dna Replication Described As Semi Conservative
Apr 01, 2025
-
Atoms That Gain Or Lose Electrons Are Called
Apr 01, 2025
-
How Many Electrons Does O Have
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Length Of In The Right Triangle Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
