What Is The Greatest Common Factor Of 9 And 4
listenit
May 25, 2025 · 5 min read
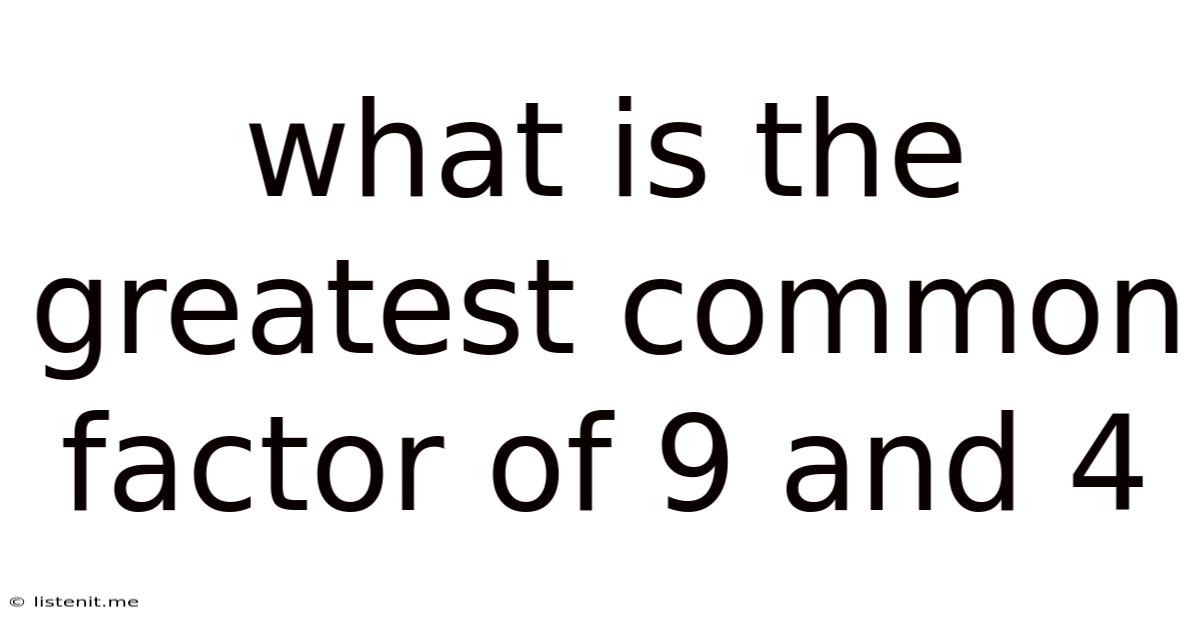
Table of Contents
What is the Greatest Common Factor of 9 and 4? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a fundamental concept in number theory with applications far beyond basic math. This article will explore the GCF of 9 and 4 in detail, demonstrating various methods for calculating it and then expanding on the broader significance of GCFs in mathematics and other fields.
Understanding Greatest Common Factors
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that fits perfectly into both numbers. For example, the GCF of 12 and 18 is 6, because 6 is the largest number that divides both 12 and 18 evenly.
Calculating the GCF of 9 and 4
Let's focus on finding the GCF of 9 and 4. We'll employ several methods to illustrate the concept and show how different approaches can lead to the same result.
Method 1: Listing Factors
The most straightforward method is listing all the factors of each number and identifying the largest common factor.
- Factors of 9: 1, 3, 9
- Factors of 4: 1, 2, 4
Comparing the two lists, we see that the only common factor is 1. Therefore, the GCF of 9 and 4 is 1.
Method 2: Prime Factorization
This method involves breaking down each number into its prime factors – prime numbers that multiply together to give the original number.
- Prime factorization of 9: 3 x 3 (or 3²)
- Prime factorization of 4: 2 x 2 (or 2²)
Since there are no common prime factors between 9 and 4, their GCF is 1. This method is particularly useful for larger numbers where listing all factors can become cumbersome.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, which is the GCF.
Let's apply the Euclidean algorithm to 9 and 4:
- 9 - 4 = 5 (Now we find the GCF of 4 and 5)
- 5 - 4 = 1 (Now we find the GCF of 4 and 1)
- Since 4 divided by 1 leaves no remainder, the GCF is 1.
Why is the GCF of 9 and 4 important?
While the GCF of 9 and 4 might seem insignificant on its own, understanding GCFs is crucial in various mathematical contexts:
-
Simplifying Fractions: The GCF helps in simplifying fractions to their lowest terms. For example, if we have the fraction 18/24, finding the GCF (which is 6) allows us to simplify it to 3/4.
-
Solving Equations: GCFs play a role in solving algebraic equations, particularly those involving polynomial expressions. Factoring polynomials often relies on finding the GCF of their terms.
-
Least Common Multiple (LCM): The GCF and LCM are closely related. The product of the GCF and LCM of two numbers is equal to the product of the two numbers. This relationship is useful in solving problems involving fractions and ratios. For 9 and 4, the LCM is 36. (9 x 4 = 36).
-
Modular Arithmetic: GCFs are fundamental in modular arithmetic, a branch of number theory where arithmetic operations are performed with remainders. This has applications in cryptography and computer science.
Real-World Applications of GCFs
Beyond theoretical mathematics, GCFs find practical applications in various fields:
-
Measurement and Division: Imagine you have two pieces of ribbon, one 9 inches long and the other 4 inches long. You want to cut them into pieces of equal length without any waste. The GCF (1 inch) tells you the largest possible length of each piece.
-
Scheduling and Planning: GCF can help in scheduling tasks or events that need to occur at regular intervals. If one event happens every 9 days and another every 4 days, finding the GCF helps determine when both events coincide again.
Expanding on the Concept of Relatively Prime Numbers
Because the GCF of 9 and 4 is 1, these numbers are considered relatively prime or coprime. This means they share no common factors other than 1. Relatively prime numbers have significant properties in number theory and various applications, such as in cryptography where the security of certain algorithms relies on the use of relatively prime numbers.
Conclusion: The Significance of a seemingly Simple Calculation
While finding the GCF of 9 and 4 might initially seem trivial, this seemingly simple calculation highlights a fundamental concept in mathematics with far-reaching implications. Understanding GCFs is not only essential for mastering arithmetic and algebra but also for appreciating the elegance and practical applications of number theory in diverse fields, ranging from simple measurement tasks to sophisticated cryptographic systems. The concept of relatively prime numbers, further illustrated by the example of 9 and 4, demonstrates an important subset of number theory, highlighting the interconnectedness of seemingly simple mathematical concepts and their broader impact. The ability to efficiently calculate and understand GCFs forms a bedrock of mathematical literacy, essential for success in many areas of study and professional endeavors.
Latest Posts
Latest Posts
-
12am To 5am Is How Many Hours
May 25, 2025
-
5 Divided By 4 As A Fraction
May 25, 2025
-
How To Calculate Volume Of A Room
May 25, 2025
-
10 Out Of 28 As A Percentage
May 25, 2025
-
2 Divided By What Equals 1 34
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 9 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.