10 Out Of 28 As A Percentage
listenit
May 25, 2025 · 5 min read
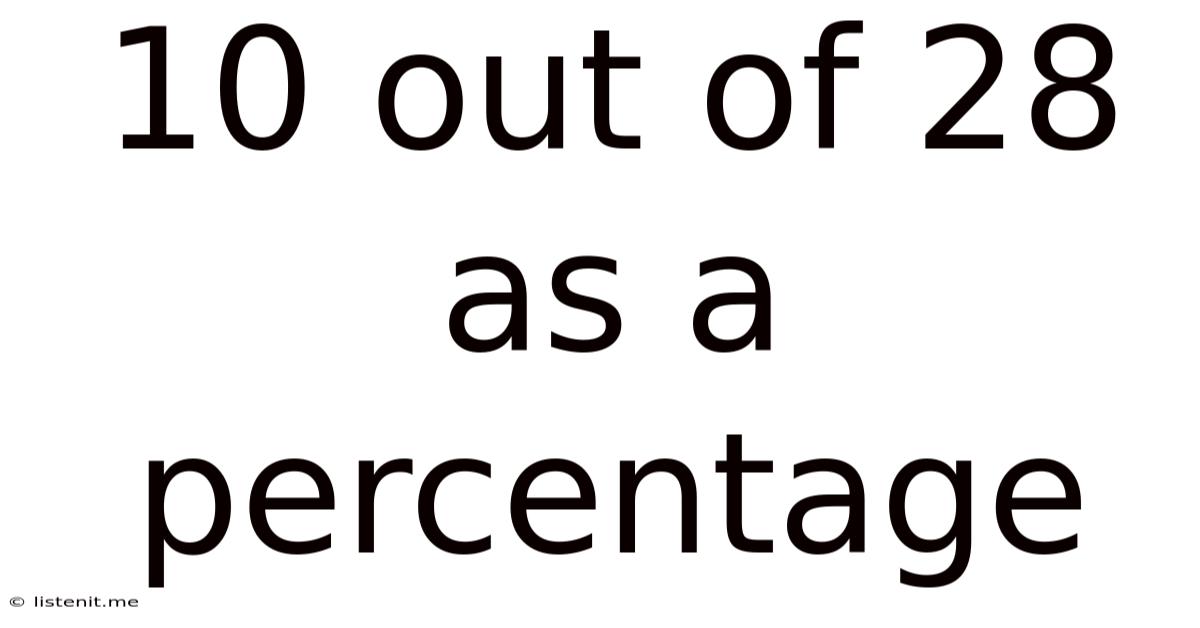
Table of Contents
10 Out of 28 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex statistical analysis. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and excelling in academic and professional settings. This comprehensive guide will delve into calculating "10 out of 28 as a percentage," exploring various methods and providing practical examples to solidify your understanding. We'll also explore the broader context of percentage calculations, empowering you to tackle similar problems with confidence.
Understanding Percentages: The Basics
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" originates from the Latin "per centum," meaning "out of one hundred." Therefore, 10% represents 10 parts out of a total of 100 parts. This fundamental understanding forms the basis for all percentage calculations.
Method 1: The Fraction Method
The most straightforward method to calculate 10 out of 28 as a percentage involves expressing the given values as a fraction and then converting it to a percentage.
Steps:
-
Form a Fraction: Represent "10 out of 28" as a fraction: 10/28.
-
Simplify the Fraction (Optional): While not strictly necessary, simplifying the fraction can make the subsequent calculations easier. Both the numerator (10) and the denominator (28) are divisible by 2, simplifying the fraction to 5/14.
-
Convert to Decimal: Divide the numerator by the denominator: 5 ÷ 14 ≈ 0.3571
-
Convert to Percentage: Multiply the decimal by 100: 0.3571 × 100 ≈ 35.71%
Therefore, 10 out of 28 is approximately 35.71%.
Method 2: Using a Calculator
Modern calculators offer a streamlined approach to percentage calculations.
Steps:
-
Divide: Enter 10 ÷ 28 into your calculator.
-
Multiply: Multiply the result by 100.
-
Interpret: The displayed value represents the percentage.
This method bypasses the manual fraction simplification and decimal conversion steps, making it quicker and less prone to errors.
Method 3: Proportion Method
The proportion method offers a different perspective on solving percentage problems.
Steps:
-
Set up a Proportion: Establish a proportion: 10/28 = x/100, where 'x' represents the unknown percentage.
-
Cross-Multiply: Cross-multiply to solve for 'x': 28x = 1000
-
Solve for x: Divide both sides by 28: x = 1000/28 ≈ 35.71
Therefore, x ≈ 35.71%, confirming our previous calculations.
Understanding the Result: 35.71%
The calculated value of 35.71% indicates that 10 represents approximately 35.71% of 28. This percentage can be interpreted in various contexts, depending on the scenario. For instance, if 10 out of 28 students passed an exam, it means that approximately 35.71% of the students were successful.
Expanding Your Percentage Calculation Skills
Mastering the calculation of "10 out of 28 as a percentage" provides a solid foundation for tackling more complex percentage problems. Let's explore some related concepts:
Calculating Percentage Increase/Decrease
Percentage increase or decrease is used to quantify the change in a value over time. The formula is:
[(New Value - Old Value) / Old Value] × 100
For example, if a value increases from 20 to 25, the percentage increase is:
[(25 - 20) / 20] × 100 = 25%
Finding the Original Value
If you know the percentage and the resulting value, you can calculate the original value. For instance, if 35.71% of a number is 10, the original number can be calculated as:
10 / (35.71/100) ≈ 28
Working with Percentages in Real-World Applications
Percentages are ubiquitous in everyday life:
- Finance: Calculating interest rates, discounts, taxes, and investment returns.
- Retail: Determining sale prices and profit margins.
- Statistics: Representing data in charts and graphs, calculating averages, and conducting statistical analyses.
- Science: Expressing concentrations, error margins, and experimental results.
Practical Applications and Examples
Let's explore some real-world scenarios where calculating percentages is essential:
Scenario 1: Exam Scores
Imagine a class of 28 students. If 10 students scored above 90%, the percentage of students achieving this score is 35.71%. This information is vital for teachers to assess class performance and adjust teaching strategies.
Scenario 2: Sales Figures
A store sold 28 items, with 10 of those being a particular product. The percentage of sales for that specific product is 35.71%. This data helps businesses understand product popularity and optimize inventory management.
Scenario 3: Survey Results
A survey of 28 people revealed that 10 prefer a certain brand. This represents a 35.71% preference rate for that brand, providing valuable market research insights.
Troubleshooting Common Mistakes
While percentage calculations are relatively straightforward, some common errors can occur:
- Incorrect Fraction Formation: Ensure you correctly represent the values as a fraction – the "part" over the "whole."
- Decimal Point Errors: Be meticulous when converting decimals to percentages and vice-versa. Double-check your calculations.
- Calculator Misuse: Familiarize yourself with your calculator's functions to avoid entering data incorrectly.
Conclusion: Mastering Percentages for Success
The ability to calculate percentages accurately is an invaluable skill. By understanding the different methods, from the fraction method to using calculators and proportions, and by practicing with real-world examples, you'll gain confidence in tackling various percentage problems. This knowledge empowers you to interpret data effectively, make informed decisions, and succeed in various aspects of life. Remember to always double-check your calculations to ensure accuracy and avoid common errors. The ability to confidently manipulate percentages will significantly enhance your analytical and problem-solving skills, providing a solid foundation for success in academic, professional, and personal endeavors. Regular practice and application of these methods will solidify your understanding and build your expertise in this essential mathematical skill.
Latest Posts
Latest Posts
-
Is 2 1 8 Equal To 1 4
May 26, 2025
-
Buy Used Or New Car Calculator
May 26, 2025
-
1 4 5 And 2 5 12
May 26, 2025
-
How Long Is 22 Hours From Now
May 26, 2025
-
8 Out Of 19 As A Percentage
May 26, 2025
Related Post
Thank you for visiting our website which covers about 10 Out Of 28 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.