What Is The Greatest Common Factor Of 36 And 54
listenit
Mar 29, 2025 · 5 min read
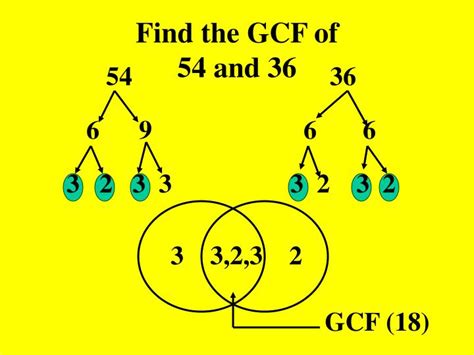
Table of Contents
What is the Greatest Common Factor of 36 and 54? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods can unlock a deeper appreciation for number theory and its applications. This comprehensive guide delves into the question: What is the greatest common factor of 36 and 54? We'll explore multiple approaches, discuss the significance of GCF, and provide examples to solidify your understanding.
Understanding Greatest Common Factor (GCF)
Before we tackle the specific numbers 36 and 54, let's define the GCF. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers.
Think of it like finding the largest shared building block of two numbers. For example, if you have 12 apples and 18 oranges, and you want to divide them into equally sized groups with no fruit left over, the largest group size you can create is 6 (two groups of 6 apples and three groups of 6 oranges). Therefore, the GCF of 12 and 18 is 6.
Methods for Finding the GCF of 36 and 54
Several methods can determine the GCF of 36 and 54. Let's examine the most common approaches:
1. Listing Factors
This method involves listing all the factors of each number and then identifying the largest common factor.
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36 Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
Comparing the two lists, we see that the common factors are 1, 2, 3, 6, 9, and 18. The greatest of these common factors is 18. Therefore, the GCF of 36 and 54 is 18.
2. Prime Factorization
Prime factorization is a powerful technique that breaks down a number into its prime factors (numbers divisible only by 1 and themselves). Once we have the prime factorization of both numbers, we can identify the GCF.
Prime factorization of 36: 2 x 2 x 3 x 3 = 2² x 3² Prime factorization of 54: 2 x 3 x 3 x 3 = 2 x 3³
To find the GCF using prime factorization, we look for the common prime factors and take the lowest power of each. Both numbers share a '2' and two '3's. Therefore:
GCF(36, 54) = 2¹ x 3² = 2 x 9 = 18
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, especially for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
- Divide the larger number (54) by the smaller number (36): 54 ÷ 36 = 1 with a remainder of 18.
- Replace the larger number with the smaller number (36) and the smaller number with the remainder (18): 36 ÷ 18 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 18.
Significance of Finding the GCF
Finding the greatest common factor isn't just an abstract mathematical exercise; it has practical applications in various fields:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 36/54 can be simplified by dividing both the numerator and denominator by their GCF (18), resulting in the simplified fraction 2/3.
-
Solving Word Problems: Many real-world problems involving division and equal sharing require finding the GCF. For instance, determining the largest possible size of identical squares that can be used to tile a rectangular area with dimensions 36 and 54 units involves finding the GCF of 36 and 54.
-
Algebra and Number Theory: GCF plays a vital role in various algebraic manipulations and number-theoretic concepts like modular arithmetic and Diophantine equations.
-
Computer Science: Algorithms for finding the GCF are used in computer science for various tasks, including cryptography and optimization problems.
Beyond 36 and 54: Extending the Concept
The methods discussed above can be applied to find the GCF of any two (or more) integers. Let's consider a few more examples:
Example 1: Finding the GCF of 48 and 72
Using prime factorization:
- 48 = 2⁴ x 3
- 72 = 2³ x 3²
GCF(48, 72) = 2³ x 3 = 8 x 3 = 24
Example 2: Finding the GCF of 120 and 180
Using the Euclidean algorithm:
- 180 ÷ 120 = 1 with a remainder of 60
- 120 ÷ 60 = 2 with a remainder of 0
GCF(120, 180) = 60
Example 3: Finding the GCF of three numbers: 24, 36, and 48
We can extend the methods to find the GCF of more than two numbers. One approach is to find the GCF of two numbers and then find the GCF of that result and the third number.
- GCF(24, 36) = 12 (using any of the methods above)
- GCF(12, 48) = 12
Therefore, GCF(24, 36, 48) = 12
Conclusion: Mastering the GCF
Understanding and mastering the concept of the greatest common factor is essential for a solid foundation in mathematics. This article explored various methods for finding the GCF, highlighting their applications and extending the concept beyond the specific case of 36 and 54. By understanding these methods and their underlying principles, you'll be well-equipped to tackle more complex number theory problems and appreciate the practical implications of this fundamental concept in various fields. Remember, practice is key – try finding the GCF of different number pairs and triplets to solidify your understanding and build your skills.
Latest Posts
Latest Posts
-
Diameter Of The Solar System In Light Years
Mar 31, 2025
-
48 Of 60 Is What Percent
Mar 31, 2025
-
Is Adenine A Purine Or Pyrimidine
Mar 31, 2025
-
A Quadrilateral With Opposite Sides Parallel
Mar 31, 2025
-
How Are Elements In The Modern Periodic Table Arranged
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 36 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
