What Is The Greatest Common Factor Of 18
listenit
May 12, 2025 · 5 min read
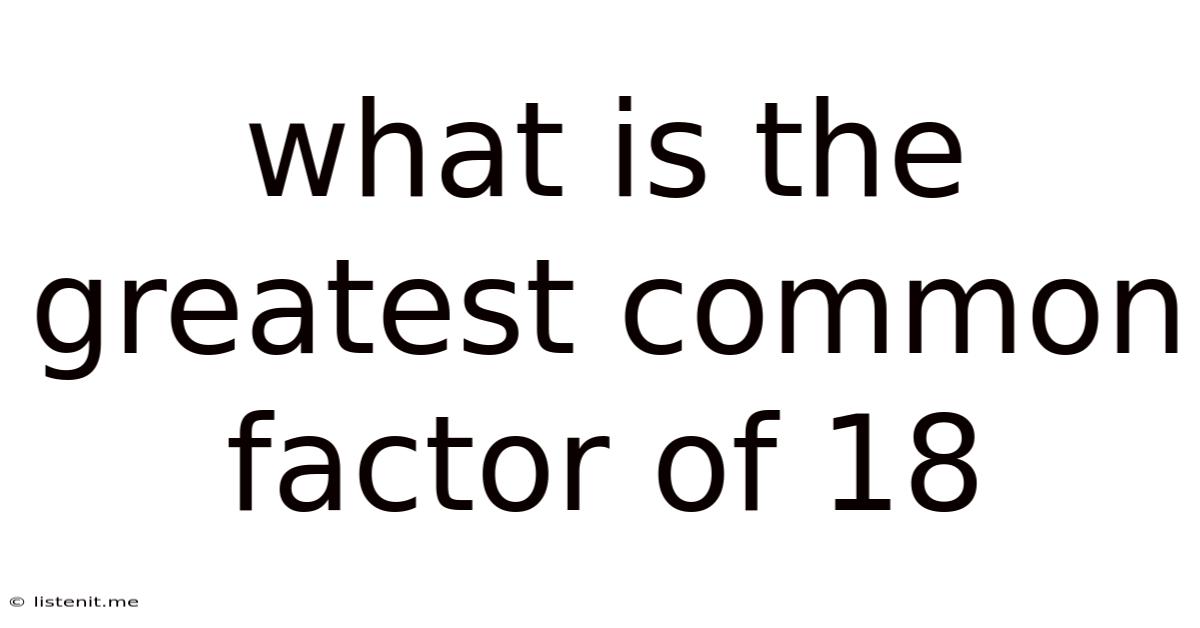
Table of Contents
What is the Greatest Common Factor of 18? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of a number might seem like a simple arithmetic task, but it's a fundamental concept in number theory with far-reaching applications in algebra, cryptography, and computer science. This article explores the GCF of 18 in detail, examining different methods for finding it and highlighting its significance within the broader mathematical landscape.
Understanding Greatest Common Factors (GCF)
Before we delve into the specific case of 18, let's establish a solid understanding of GCFs. The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides all the numbers in question.
For example, let's consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF(12, 18) = 6.
Finding the GCF of 18: A Single Number Scenario
The question "What is the greatest common factor of 18?" is slightly different from finding the GCF of two or more numbers. When we're asked for the GCF of a single number, we're essentially looking for its largest factor. This is because the GCF only makes sense in the context of comparing multiple numbers. A single number is always divisible by itself and 1.
Therefore, the greatest common factor of 18 is 18. There's no other number larger than 18 that can divide 18 evenly without leaving a remainder. It might seem trivial, but understanding this nuance is critical.
Methods for Finding GCFs (Applicable when comparing multiple numbers)
While the GCF of 18 alone is 18, let's explore methods for finding GCFs when dealing with multiple numbers, as this is where the concept truly shines:
1. Listing Factors Method
This is a straightforward approach, particularly suitable for smaller numbers. You list all the factors of each number, then identify the common factors and select the largest one.
Let's find the GCF of 18 and 24 using this method:
- Factors of 18: 1, 2, 3, 6, 9, 18
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
The common factors are 1, 2, 3, and 6. The GCF(18, 24) = 6.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves breaking down each number into its prime factors (numbers divisible only by 1 and themselves).
Let's find the GCF of 18 and 24 using prime factorization:
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
- Prime factorization of 24: 2 x 2 x 2 x 3 = 2³ x 3
The common prime factors are 2 and 3. To find the GCF, we take the lowest power of each common prime factor:
GCF(18, 24) = 2¹ x 3¹ = 6
3. Euclidean Algorithm
This is a highly efficient algorithm, particularly useful for very large numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's find the GCF(18, 24) using the Euclidean Algorithm:
- 24 = 18 x 1 + 6 (Subtract 18 from 24, leaving a remainder of 6)
- 18 = 6 x 3 + 0 (Divide 18 by 6; the remainder is 0)
Since the remainder is 0, the GCF is the last non-zero remainder, which is 6.
The Significance of GCFs
The GCF is more than just a mathematical curiosity; it has numerous practical applications:
-
Simplifying Fractions: Finding the GCF allows us to simplify fractions to their lowest terms. For example, the fraction 18/24 can be simplified to 3/4 by dividing both the numerator and denominator by their GCF (6).
-
Solving Problems Involving Ratios and Proportions: GCFs are essential in simplifying ratios and working with proportions in various fields, such as cooking, construction, and engineering.
-
Algebra and Polynomial Division: GCFs play a crucial role in factoring polynomials and simplifying algebraic expressions.
-
Cryptography: The concept of GCFs is fundamental to many cryptographic algorithms, particularly those based on modular arithmetic.
-
Computer Science: GCF calculations are used in algorithms for data compression, graph theory, and other computational tasks.
GCF and the Least Common Multiple (LCM)
The GCF and the least common multiple (LCM) are closely related concepts. The LCM is the smallest positive integer that is a multiple of each of the given integers. There's a useful relationship between the GCF and LCM of two numbers (a and b):
GCF(a, b) x LCM(a, b) = a x b
This formula provides a convenient way to calculate the LCM if you already know the GCF (or vice-versa).
Conclusion: The Importance of Understanding Fundamental Concepts
The greatest common factor of 18, while seemingly simple, serves as a gateway to understanding more complex mathematical concepts. Mastering GCF calculations is not just about finding the largest divisor; it’s about grasping a fundamental building block of number theory with wide-ranging applications in various fields. By understanding the different methods for finding GCFs – the listing factors method, prime factorization, and the Euclidean algorithm – you equip yourself with valuable tools for solving a variety of mathematical problems and appreciate the underlying structure of numbers. This knowledge is crucial for success in higher-level mathematics and related disciplines. The seemingly simple question, "What is the greatest common factor of 18?" opens a door to a rich and fascinating area of mathematics.
Latest Posts
Latest Posts
-
One Result Of The Neolithic Revolution Was
May 12, 2025
-
Solve The Formula D Rt For R
May 12, 2025
-
A Tool Used To Measure Volume
May 12, 2025
-
Butene Would Have Carbon Atoms And A Bond
May 12, 2025
-
18 Is 60 Percent Of What Number
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.