18 Is 60 Percent Of What Number
listenit
May 12, 2025 · 4 min read
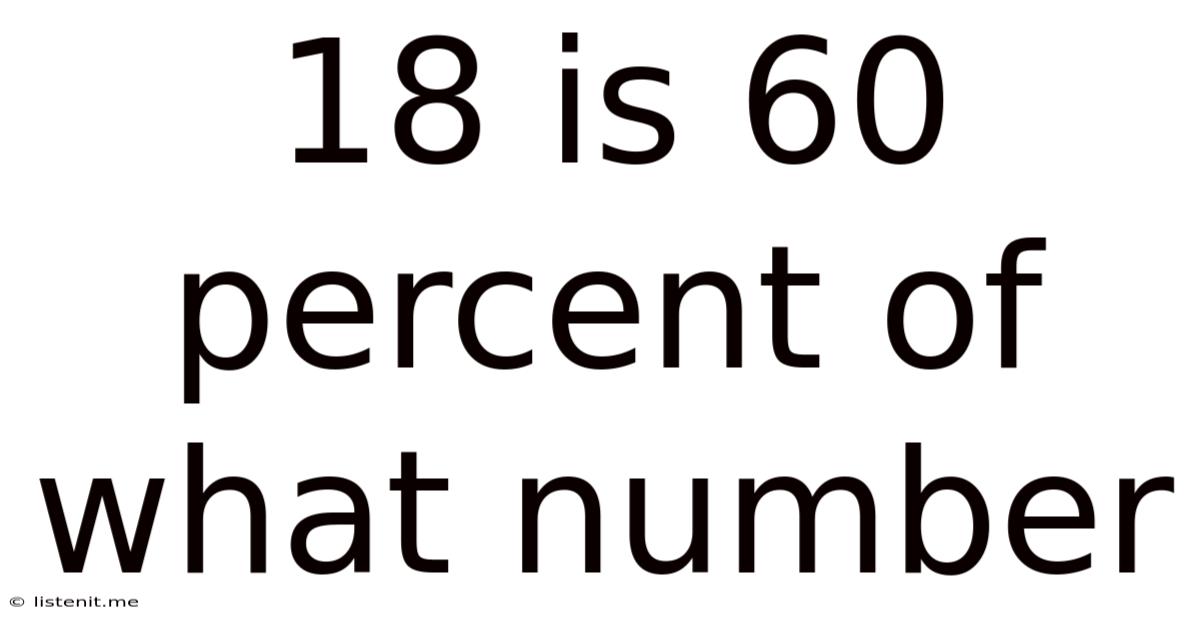
Table of Contents
18 is 60 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill applicable across various fields, from everyday budgeting and shopping to complex scientific calculations and business analytics. Understanding how to determine the base number when given a percentage and its value is crucial. This article provides a comprehensive guide to solving problems like "18 is 60 percent of what number?", explaining the underlying concepts, various solution methods, and practical applications.
Understanding the Basics of Percentages
A percentage is a fraction or ratio expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100." To convert a percentage to a decimal, simply divide the percentage by 100. For example, 60% is equivalent to 60/100 = 0.6. Conversely, to convert a decimal to a percentage, multiply the decimal by 100.
Different Approaches to Solving "18 is 60% of What Number?"
There are several methods to solve this type of problem. We'll explore three common approaches:
Method 1: Using the Percentage Formula
The fundamental percentage formula is:
(Percentage/100) * Base Number = Part
Where:
- Percentage is the percentage value (in our case, 60%).
- Base Number is the total value we want to find (the unknown).
- Part is the given portion of the base number (in our case, 18).
Let's apply this formula to our problem:
(60/100) * x = 18
To solve for 'x' (the base number), follow these steps:
- Convert the percentage to a decimal: 60/100 = 0.6
- Rewrite the equation: 0.6x = 18
- Isolate 'x' by dividing both sides by 0.6: x = 18 / 0.6
- Calculate the result: x = 30
Therefore, 18 is 60% of 30.
Method 2: Using Proportions
This method involves setting up a proportion:
Part/Base Number = Percentage/100
Substituting our values:
18/x = 60/100
To solve for 'x', cross-multiply:
18 * 100 = 60 * x
1800 = 60x
Divide both sides by 60:
x = 1800 / 60
x = 30
Again, we find that 18 is 60% of 30.
Method 3: Using the "Is-Of-Percent" Method
This method is a more intuitive approach, helpful for visualizing the problem:
"18 is 60% of what number?" can be translated into:
18 = 0.6 * x
Solving for x:
x = 18 / 0.6
x = 30
Practical Applications of Percentage Calculations
Understanding percentage calculations has numerous real-world applications:
1. Finance and Budgeting:
- Calculating discounts: If an item is discounted by 20%, you can easily determine the final price.
- Calculating interest: Determining simple or compound interest on loans or investments.
- Analyzing financial statements: Understanding profit margins, revenue growth, and expense ratios.
- Tax calculations: Computing income tax, sales tax, or VAT.
2. Business and Sales:
- Profit margin analysis: Determining the profitability of products or services.
- Sales target setting: Setting realistic sales goals based on past performance and market trends.
- Market share analysis: Assessing a company's position within a particular market.
- Pricing strategies: Setting competitive prices that maximize profit.
3. Science and Research:
- Data analysis: Presenting and interpreting data in a meaningful way using percentages.
- Statistical analysis: Calculating probabilities and confidence intervals.
- Experimental design: Determining sample sizes and analyzing results.
4. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in restaurants or for services rendered.
- Understanding nutritional information: Analyzing the percentage of daily recommended values on food labels.
- Comparing prices: Determining the best value for money when comparing similar products.
- Estimating quantities: Calculating proportions for cooking or construction projects.
Expanding Your Understanding: More Complex Percentage Problems
While the problem "18 is 60% of what number?" is relatively straightforward, understanding the underlying principles allows you to tackle more complex percentage problems. These often involve multiple steps and may require a deeper understanding of algebraic manipulation. For example, you might encounter scenarios where you need to:
- Calculate percentage change: Determining the increase or decrease in a value over time. (e.g., "Sales increased by 15% from last year.")
- Calculate percentage points: Understanding the difference between percentage change and percentage points. (e.g., "Interest rates rose from 2% to 5%, an increase of 3 percentage points, not 150%")
- Solve problems involving multiple percentages: Calculating successive discounts or interest rates. (e.g., "A 20% discount followed by a 10% discount.")
- Work with percentages and other mathematical operations: Combining percentage calculations with addition, subtraction, multiplication, and division.
Mastering Percentage Calculations: Practice Makes Perfect
The key to mastering percentage calculations is consistent practice. Start with simple problems like "18 is 60% of what number?" and gradually progress to more complex scenarios. Use online resources, textbooks, or practice worksheets to reinforce your understanding. The more you practice, the more comfortable and efficient you'll become at solving percentage problems. Regular practice will not only improve your problem-solving skills but also enhance your overall mathematical fluency. This will be invaluable in various aspects of your personal and professional life. Remember, accuracy and a methodical approach are paramount in achieving correct results. Don't be afraid to break down complex problems into smaller, more manageable steps. By employing the methods outlined in this article, consistently practicing, and adopting a structured approach, you can master percentage calculations and confidently apply them to a wide array of situations.
Latest Posts
Latest Posts
-
What Is The Value Of Log4 16
May 12, 2025
-
For What Values Of Th Is Tanth Undefined
May 12, 2025
-
Which Of The Following Is An Example Of Electromagnetic Waves
May 12, 2025
-
What Is 7 To The Power Of 5
May 12, 2025
-
How Is The Sun Different From Other Stars
May 12, 2025
Related Post
Thank you for visiting our website which covers about 18 Is 60 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.