What Is 7 To The Power Of 5
listenit
May 12, 2025 · 6 min read
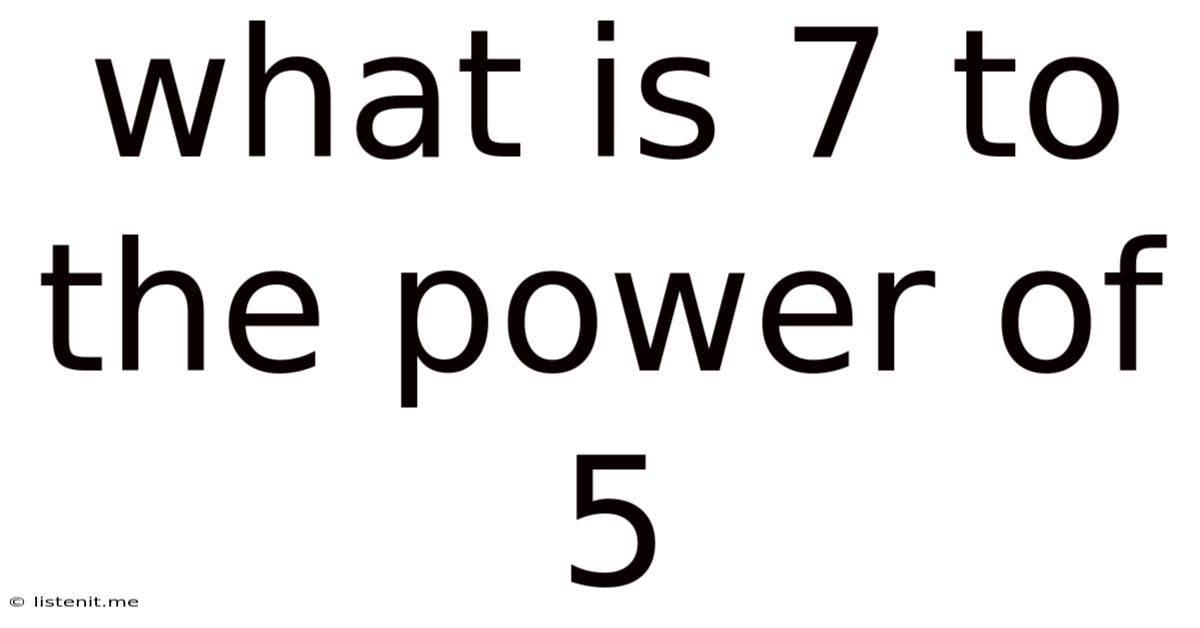
Table of Contents
What is 7 to the Power of 5? A Deep Dive into Exponentiation
The seemingly simple question, "What is 7 to the power of 5?" opens a door to a fascinating world of mathematics, specifically exponentiation. While a calculator can quickly provide the answer (16807), understanding the underlying concepts offers a richer appreciation of mathematical principles and their practical applications. This article will explore not just the answer, but the meaning of exponentiation, its properties, related mathematical concepts, and even some surprising real-world applications.
Understanding Exponentiation: Beyond Simple Multiplication
Exponentiation, at its core, is repeated multiplication. The expression 7<sup>5</sup> means 7 multiplied by itself five times: 7 × 7 × 7 × 7 × 7. The base number (7) is the number being multiplied, and the exponent (5) indicates how many times the base is multiplied by itself. This seemingly simple operation has profound implications across various mathematical fields.
Key Terminology: Base and Exponent
- Base: The number being raised to a power (in this case, 7).
- Exponent: The number indicating how many times the base is multiplied by itself (in this case, 5). Also known as the power or index.
Understanding these terms is crucial for grasping the concept of exponentiation and working with exponential expressions.
Calculating 7 to the Power of 5: Step-by-Step
Let's break down the calculation of 7<sup>5</sup> step-by-step to solidify our understanding:
- 7 × 7 = 49: Our first multiplication.
- 49 × 7 = 343: The result of the first multiplication is multiplied by 7 again.
- 343 × 7 = 2401: Continuing the pattern.
- 2401 × 7 = 16807: The final multiplication yields the answer.
Therefore, 7 to the power of 5 is 16807.
Properties of Exponents: Expanding Our Understanding
Exponentiation possesses several key properties that are fundamental to algebraic manipulation and problem-solving. These properties allow us to simplify complex expressions and solve equations more efficiently.
Product of Powers
When multiplying two numbers with the same base raised to different powers, we add the exponents: a<sup>m</sup> × a<sup>n</sup> = a<sup>m+n</sup>. For instance, 7<sup>2</sup> × 7<sup>3</sup> = 7<sup>2+3</sup> = 7<sup>5</sup> = 16807.
Quotient of Powers
When dividing two numbers with the same base raised to different powers, we subtract the exponents: a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>. This only applies if a ≠ 0. For example, 7<sup>5</sup> / 7<sup>2</sup> = 7<sup>5-2</sup> = 7<sup>3</sup> = 343.
Power of a Power
When raising a power to another power, we multiply the exponents: (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup>. For example, (7<sup>2</sup>)<sup>3</sup> = 7<sup>2×3</sup> = 7<sup>6</sup> = 117649.
Power of a Product
When raising a product to a power, we raise each factor to that power: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>. For example, (2 × 7)<sup>3</sup> = 2<sup>3</sup> × 7<sup>3</sup> = 8 × 343 = 2744.
Power of a Quotient
Similarly, when raising a quotient to a power, we raise both the numerator and denominator to that power: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup> (where b ≠ 0). For example, (7/2)<sup>2</sup> = 7<sup>2</sup>/2<sup>2</sup> = 49/4 = 12.25.
Beyond the Basics: Exploring Related Mathematical Concepts
The concept of exponentiation extends far beyond simple calculations. It forms the foundation for several crucial mathematical concepts:
Scientific Notation
Scientific notation uses exponents to represent very large or very small numbers concisely. For instance, the speed of light (approximately 299,792,458 meters per second) can be written in scientific notation as 2.99792458 × 10<sup>8</sup> m/s.
Logarithms
Logarithms are the inverse operation of exponentiation. The logarithm base b of a number x (written as log<sub>b</sub>x) is the exponent to which b must be raised to produce x. For example, log<sub>7</sub>16807 = 5 because 7<sup>5</sup> = 16807. Logarithms are crucial in various fields, including physics, chemistry, and engineering.
Exponential Functions and Growth/Decay
Exponential functions are functions where the variable appears in the exponent. These functions model exponential growth (e.g., population growth, compound interest) and exponential decay (e.g., radioactive decay, cooling of an object). Understanding exponential functions is vital in various scientific and financial models.
Real-World Applications of Exponentiation: From Finance to Physics
Exponentiation is not just a mathematical abstraction; it has numerous practical applications in various fields:
Finance: Compound Interest
Compound interest calculations heavily rely on exponentiation. The formula for compound interest is A = P(1 + r/n)<sup>nt</sup>, where:
- A = the future value of the investment/loan, including interest.
- P = the principal investment amount (the initial deposit or loan amount).
- r = the annual interest rate (decimal).
- n = the number of times that interest is compounded per year.
- t = the number of years the money is invested or borrowed for.
The exponent nt determines the effect of compounding over time. The more frequent the compounding (larger n), the faster the growth.
Computer Science: Binary Numbers and Data Storage
Computers use binary numbers (base-2), where exponentiation is essential for representing numbers and calculating memory addresses. Each bit in a computer's memory represents a power of 2. For example, 8 bits (a byte) can represent 2<sup>8</sup> = 256 different values.
Physics: Radioactive Decay
Radioactive decay follows an exponential decay model. The amount of a radioactive substance remaining after a certain time can be calculated using an exponential function. This is crucial in various fields, including nuclear medicine and environmental science.
Biology: Population Growth
Population growth, under ideal conditions, often follows an exponential pattern. Understanding exponential growth models is vital for predicting population sizes and managing resources.
Conclusion: The Power of Understanding Exponentiation
While the answer to "What is 7 to the power of 5?" is simply 16807, the journey to arrive at this answer unveils a wealth of mathematical concepts and their real-world applications. Exponentiation is a fundamental building block in numerous fields, from finance and computer science to physics and biology. A deep understanding of exponentiation, its properties, and related concepts equips us with the tools to solve complex problems and appreciate the power of mathematics in shaping our world. The seemingly simple calculation of 7<sup>5</sup> serves as a gateway to a broader appreciation of mathematical principles and their significant impact on our daily lives. From understanding compound interest to comprehending the intricacies of radioactive decay, exponentiation underpins many critical aspects of our modern world. Therefore, mastering this concept opens doors to a deeper understanding of the mathematical universe around us.
Latest Posts
Latest Posts
-
Substance That Cannot Be Broken Down
May 13, 2025
-
Does Period Go Before Or After Quotes
May 13, 2025
-
What Is The Monomer Used To Make Protein
May 13, 2025
-
Identify The Center And Radius Of The Circle
May 13, 2025
-
What Do Earth And The Moon Have In Common
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 7 To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.