What Is The Gcf Of 8 And 14
listenit
May 24, 2025 · 5 min read
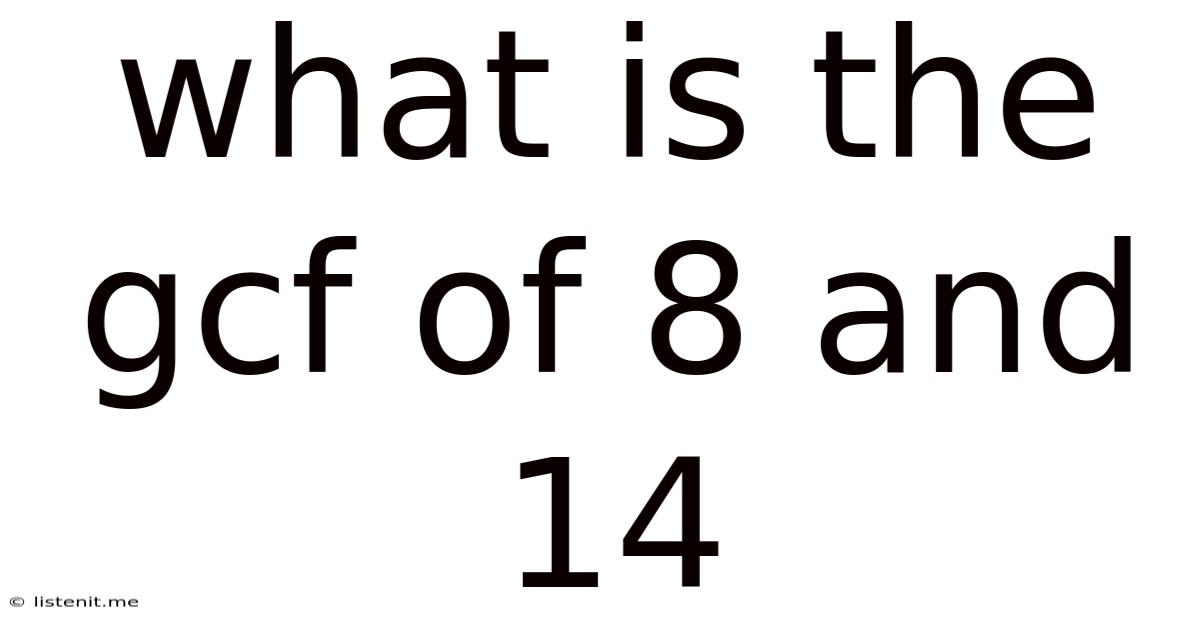
Table of Contents
What is the GCF of 8 and 14? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods can reveal a wealth of mathematical insights. This article delves into the question: What is the GCF of 8 and 14? We'll not only answer this question but also explore various techniques to find the GCF, discuss the importance of GCF in mathematics and real-world applications, and provide you with the tools to confidently tackle similar problems.
Understanding Greatest Common Factors (GCF)
Before we determine the GCF of 8 and 14, let's define what a greatest common factor is. The GCF, also known as greatestcommon divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can be divided evenly into both numbers.
Think of it like finding the largest shared building block of two numbers. For example, if you have 12 apples and 18 oranges, and you want to divide them into equal groups without any leftovers, the largest group size you can make is 6 (each group would have 2 apples and 3 oranges). Therefore, the GCF of 12 and 18 is 6.
Methods for Finding the GCF
Several methods exist to find the greatest common factor. Let's explore the most common ones:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 8: 1, 2, 4, 8
- Factors of 14: 1, 2, 7, 14
Comparing the two lists, we see that the common factors are 1 and 2. The largest of these common factors is 2.
Therefore, using the listing factors method, the GCF of 8 and 14 is 2.
2. Prime Factorization Method
This method is particularly useful for larger numbers. It involves finding the prime factorization of each number and then identifying the common prime factors.
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 14: 2 x 7
The only common prime factor is 2. Therefore, the GCF is 2.
This method reinforces the concept of prime numbers as the fundamental building blocks of all other integers. By breaking down the numbers into their prime components, we can easily identify shared elements. This approach is efficient and provides a deeper understanding of the number's structure.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to 8 and 14:
- 14 ÷ 8 = 1 with a remainder of 6
- 8 ÷ 6 = 1 with a remainder of 2
- 6 ÷ 2 = 3 with a remainder of 0
The last non-zero remainder is 2, so the GCF of 8 and 14 is 2.
The Significance of GCF
Understanding GCFs is crucial in various areas of mathematics and its applications:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For instance, the fraction 8/14 can be simplified to 4/7 by dividing both the numerator and denominator by their GCF, which is 2.
-
Solving Word Problems: GCF frequently appears in word problems involving dividing items into equal groups, distributing resources fairly, or determining the largest possible size of a square tile to cover a rectangular area.
-
Algebra and Number Theory: GCF plays a vital role in advanced mathematical concepts such as modular arithmetic, Diophantine equations, and abstract algebra.
-
Computer Science: Algorithms for finding GCF are essential in cryptography and other areas of computer science where efficient computations are crucial.
Real-World Applications of GCF
The GCF isn't just a theoretical concept; it has practical applications in daily life:
-
Baking: If you have 8 cups of flour and 14 cups of sugar, and you want to divide the ingredients equally among batches of cookies, the GCF (2) will tell you that you can make 2 batches of cookies, using 4 cups of flour and 7 cups of sugar per batch.
-
Gardening: If you have an 8-foot by 14-foot rectangular garden, and you want to divide it into equal square plots, the GCF (2) indicates that the largest possible square plot size is 2 feet by 2 feet.
-
Construction: GCF helps determine the size of the largest common tile or brick to cover a surface area with no gaps or overlaps.
-
Manufacturing: Understanding GCF is useful when determining the maximum size of identical components that can be cut from a larger piece of material.
Expanding the Concept: Beyond Two Numbers
While we've focused on finding the GCF of two numbers, the concept extends to finding the GCF of three or more numbers. The methods described earlier, especially prime factorization and the Euclidean algorithm (which can be adapted for multiple numbers), are easily applicable to multiple number scenarios.
Conclusion: Mastering GCF
Finding the GCF of 8 and 14, which is 2, is a straightforward exercise. However, understanding the various methods – listing factors, prime factorization, and the Euclidean algorithm – provides a comprehensive grasp of the concept and its applications. Mastering GCF enhances your mathematical skills, enabling you to solve complex problems efficiently and effectively in various fields. From simplifying fractions to solving real-world challenges involving equal division and resource allocation, the ability to find the greatest common factor is an invaluable asset. Remember, the key is to choose the method that best suits the numbers involved and your understanding of the concept. By practicing these methods, you will not only be able to quickly calculate GCFs but also develop a deeper appreciation for the beauty and power of mathematics.
Latest Posts
Latest Posts
-
What Is 20 Off Of 36
May 24, 2025
-
1 5 10 As A Decimal
May 24, 2025
-
Common Factors Of 50 And 80
May 24, 2025
-
5 Is What Percent Of 23
May 24, 2025
-
Add 14 And 13 Then Divide By 3
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 8 And 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.