What Is The Gcf Of 7 And 28
listenit
May 24, 2025 · 5 min read
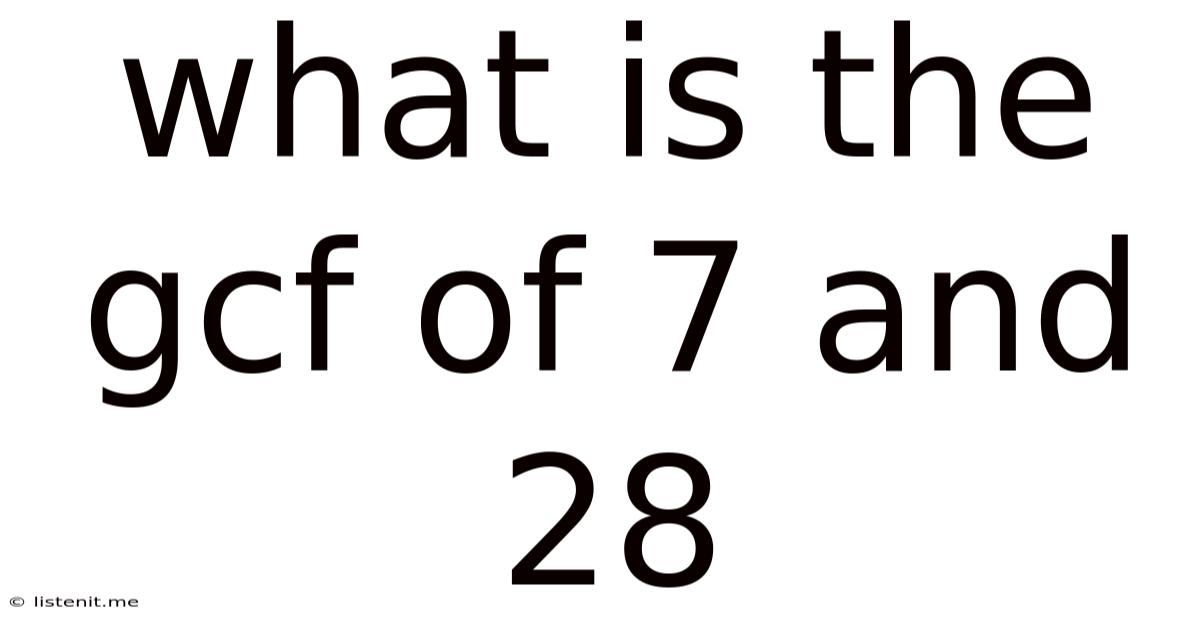
Table of Contents
What is the GCF of 7 and 28? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it lays a strong foundation for more advanced mathematical concepts. This article will not only answer the question, "What is the GCF of 7 and 28?" but also explore the broader world of GCFs, offering multiple approaches to solving such problems and highlighting their real-world applications.
Understanding Greatest Common Factors (GCF)
Before delving into the specifics of finding the GCF of 7 and 28, let's define the term. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers.
This concept is fundamental in various areas of mathematics, including:
- Simplifying fractions: Finding the GCF allows you to reduce fractions to their simplest form.
- Algebraic expressions: GCF is crucial for factoring algebraic expressions, making them easier to solve and analyze.
- Number theory: GCF plays a significant role in advanced number theory concepts like modular arithmetic and cryptography.
Methods for Finding the GCF
Several methods exist for determining the GCF of two or more numbers. Let's explore the most common ones:
1. Listing Factors
This is the most straightforward method, especially for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 7: 1, 7 Factors of 28: 1, 2, 4, 7, 14, 28
The common factors are 1 and 7. Therefore, the GCF of 7 and 28 is 7.
2. Prime Factorization
This method involves breaking down each number into its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 28: 2 x 2 x 7 = 2² x 7
The only common prime factor is 7, and it appears with a power of 1 in both factorizations. Therefore, the GCF of 7 and 28 is 7.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 7 and 28:
- 28 - 7 = 21
- 21 - 7 = 14
- 14 - 7 = 7
- 7 - 7 = 0
The process stops when the difference is 0. The last non-zero remainder is the GCF, which is 7.
4. Ladder Method (or Staircase Method)
This is a visual way to represent the Euclidean algorithm, making it easier to follow.
28 | 7
21 | 7
14 | 7
7 | 7
0
We repeatedly subtract the smaller number from the larger number until we reach 0. The last non-zero number is the GCF, which is 7.
Why is the GCF Important? Real-World Applications
The concept of the greatest common factor extends far beyond simple arithmetic exercises. Its applications are widespread and crucial in various fields:
1. Simplifying Fractions
GCF is essential for simplifying fractions to their lowest terms. For example, the fraction 28/7 can be simplified by dividing both the numerator and denominator by their GCF (7):
28/7 = (28 ÷ 7) / (7 ÷ 7) = 4/1 = 4
2. Geometry and Measurement
GCF is used when dealing with measurements and shapes. Imagine you need to cut a piece of cloth of length 28 cm and another of 7 cm into smaller pieces of equal length, with the pieces being as long as possible. The GCF (7 cm) will determine the maximum length of the pieces.
3. Algebra and Factoring
GCF is a fundamental tool in algebra for factoring polynomials. Factoring simplifies algebraic expressions, making them easier to solve and manipulate.
4. Cryptography and Number Theory
GCF is a cornerstone of number theory and cryptographic algorithms. For instance, the Euclidean algorithm plays a vital role in the RSA algorithm, a widely used public-key cryptosystem ensuring secure data transmission.
Beyond Two Numbers: Finding the GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For example, to find the GCF of 7, 28, and 42:
-
Prime Factorization:
- 7 = 7
- 28 = 2² x 7
- 42 = 2 x 3 x 7
The common prime factor is 7, and its lowest power is 1. Therefore, the GCF of 7, 28, and 42 is 7.
-
Euclidean Algorithm (extended): You could find the GCF of two numbers (say, 7 and 28), and then find the GCF of the result and the third number (42).
Conclusion: The Power of the GCF
In conclusion, the GCF of 7 and 28 is undeniably 7. Understanding how to find the GCF using different methods isn't just about mastering a specific arithmetic skill; it's about grasping a fundamental concept that permeates various areas of mathematics and its real-world applications. From simplifying fractions to securing online transactions, the GCF plays a surprisingly significant role in our daily lives, proving its importance beyond the classroom. This exploration into the GCF highlights its versatility and its impact on various mathematical and practical scenarios. Mastering this concept forms a solid basis for tackling more complex mathematical challenges.
Latest Posts
Latest Posts
-
25 7 Is What Percent Of 141
May 24, 2025
-
What Day Of The Week Is December 3
May 24, 2025
-
80 Trillion Divided By 8 Billion
May 24, 2025
-
Least Common Multiple Of 14 And 24
May 24, 2025
-
15 Meters Per Second To Mph
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 7 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.