What Is The Gcf Of 45 And 75
listenit
Apr 02, 2025 · 6 min read
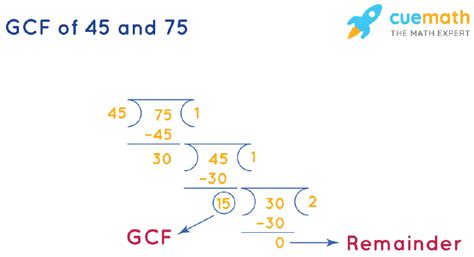
Table of Contents
What is the GCF of 45 and 75? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods to arrive at the solution opens up a fascinating world of number theory. This comprehensive guide will not only answer the question, "What is the GCF of 45 and 75?" but will also equip you with the knowledge and skills to tackle similar problems with confidence. We'll explore various methods, delve into the importance of GCFs, and show you how this concept extends beyond simple arithmetic.
Understanding Greatest Common Factors (GCF)
Before we dive into finding the GCF of 45 and 75, let's establish a solid foundation. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
For example, consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF of 12 and 18 is 6.
Methods for Finding the GCF
Several methods can be employed to find the GCF of two numbers. We will explore three popular approaches:
1. Listing Factors
This is the most straightforward method, especially for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
Let's apply this to find the GCF of 45 and 75:
- Factors of 45: 1, 3, 5, 9, 15, 45
- Factors of 75: 1, 3, 5, 15, 25, 75
Comparing the two lists, we see that the common factors are 1, 3, 5, and 15. The greatest of these is 15. Therefore, the GCF of 45 and 75 is 15.
While this method is simple for smaller numbers, it can become cumbersome and time-consuming for larger numbers.
2. Prime Factorization
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. The steps are as follows:
-
Find the prime factorization of each number. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
- Prime factorization of 45: 3 x 3 x 5 = 3² x 5
- Prime factorization of 75: 3 x 5 x 5 = 3 x 5²
-
Identify the common prime factors. In this case, both 45 and 75 share a 3 and a 5.
-
Multiply the common prime factors to find the GCF. The common prime factors are 3 and 5. Multiplying them together gives us 3 x 5 = 15. Therefore, the GCF of 45 and 75 is 15.
This method is more efficient than listing factors, especially when dealing with larger numbers.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It relies on repeated application of the division algorithm. The steps are as follows:
-
Divide the larger number by the smaller number and find the remainder. 75 ÷ 45 = 1 with a remainder of 30.
-
Replace the larger number with the smaller number and the smaller number with the remainder. Now we have 45 and 30.
-
Repeat the process until the remainder is 0.
- 45 ÷ 30 = 1 with a remainder of 15
- 30 ÷ 15 = 2 with a remainder of 0
-
The last non-zero remainder is the GCF. In this case, the last non-zero remainder is 15. Therefore, the GCF of 45 and 75 is 15.
The Euclidean algorithm is particularly efficient because it avoids the need to find all the factors of the numbers involved.
Applications of GCF
Understanding and calculating the GCF is not just an academic exercise; it has practical applications in various fields:
-
Simplifying Fractions: Finding the GCF allows you to simplify fractions to their lowest terms. For example, the fraction 45/75 can be simplified to 3/5 by dividing both the numerator and denominator by their GCF, which is 15.
-
Solving Word Problems: Many word problems in mathematics involve finding the GCF. For instance, if you have 45 apples and 75 oranges, and you want to divide them into identical bags with the maximum number of fruits in each bag, the GCF (15) tells you the maximum number of bags you can create. Each bag will have 3 apples and 5 oranges.
-
Geometry and Measurement: GCF plays a crucial role in geometry problems involving finding the dimensions of squares or rectangles with the largest possible side lengths.
-
Computer Science: The Euclidean algorithm, used to find the GCF, is a fundamental algorithm in computer science, utilized in cryptography and other areas.
-
Music Theory: GCF is also used in music theory to determine the greatest common divisor of two note intervals. This determines the simplified ratio between the frequencies of the notes, which helps in understanding musical harmony.
Beyond Two Numbers: Finding the GCF of More Than Two Numbers
The methods discussed above can be extended to find the GCF of more than two numbers. For example, to find the GCF of 45, 75, and 90, you can use any of the above-mentioned methods to first find the GCF of any two numbers and then find the GCF of the resulting number and the third number. Using prime factorization:
- 45 = 3² x 5
- 75 = 3 x 5²
- 90 = 2 x 3² x 5
The common prime factors are 3 and 5. Therefore the GCF of 45, 75, and 90 is 3 x 5 = 15.
Or, you could use the Euclidean algorithm iteratively. First, find the GCF of 45 and 75 (which is 15), and then find the GCF of 15 and 90 (which is also 15).
Conclusion: Mastering GCF for Enhanced Mathematical Understanding
This comprehensive exploration of the greatest common factor has not only answered the initial question regarding the GCF of 45 and 75 (which is 15) but has also equipped you with a deeper understanding of the concept and its various applications. By mastering the different methods for finding the GCF – listing factors, prime factorization, and the Euclidean algorithm – you will be better prepared to tackle a wide range of mathematical problems and enhance your overall mathematical proficiency. Remember, the choice of method depends on the numbers involved and personal preference; for smaller numbers, listing factors might suffice, while for larger numbers, prime factorization or the Euclidean algorithm prove more efficient. The understanding of GCF extends far beyond simple arithmetic, opening doors to a more profound appreciation of number theory and its practical applications in various fields.
Latest Posts
Latest Posts
-
What Is The Symbol For Population Variance
Apr 03, 2025
-
What Is A Reactant In Photosynthesis
Apr 03, 2025
-
32 Of 40 Percent Is What Number
Apr 03, 2025
-
What Is Found In Plant Cells But Not Animal Cells
Apr 03, 2025
-
What Percent Of 9 2 Is 43 7
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 45 And 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
