What Is The Gcf Of 28 And 24
listenit
Mar 26, 2025 · 5 min read
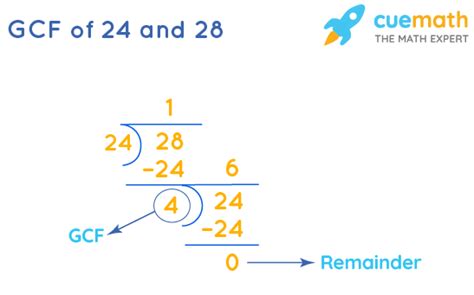
Table of Contents
- What Is The Gcf Of 28 And 24
- Table of Contents
- What is the GCF of 28 and 24? A Deep Dive into Greatest Common Factors
- Understanding Greatest Common Factors (GCF)
- Finding the GCF of 28 and 24: Method 1 - Listing Factors
- Finding the GCF of 28 and 24: Method 2 - Prime Factorization
- Finding the GCF of 28 and 24: Method 3 - Euclidean Algorithm
- Applications of GCF in Real-World Scenarios
- Expanding on the Concept: GCF of More Than Two Numbers
- Why Understanding GCF is Important
- Conclusion: The Power of the GCF
- Latest Posts
- Latest Posts
- Related Post
What is the GCF of 28 and 24? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it can be incredibly valuable, especially in fields like algebra, number theory, and even computer science. This comprehensive guide will explore the GCF of 28 and 24, explaining not just the answer but also the why behind the calculations, and offering multiple approaches to finding the GCF for any pair of numbers.
Understanding Greatest Common Factors (GCF)
Before we delve into the specifics of 28 and 24, let's establish a solid foundation. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the two or more numbers without leaving a remainder. Think of it as the biggest number that perfectly fits into both numbers.
Key Concepts:
- Factors: Factors are numbers that divide another number exactly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
- Common Factors: Common factors are factors that are shared by two or more numbers. For instance, the common factors of 12 and 18 are 1, 2, 3, and 6.
- Greatest Common Factor (GCF): The GCF is simply the largest of these common factors. In the case of 12 and 18, the GCF is 6.
Finding the GCF of 28 and 24: Method 1 - Listing Factors
The most straightforward method, especially for smaller numbers, is to list all the factors of each number and then identify the largest common factor.
Factors of 28: 1, 2, 4, 7, 14, 28
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Comparing the two lists, we see that the common factors are 1, 2, and 4. The largest of these is 4.
Therefore, the GCF of 28 and 24 is 4.
Finding the GCF of 28 and 24: Method 2 - Prime Factorization
Prime factorization involves breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). This method is particularly useful for larger numbers where listing all factors becomes cumbersome.
Prime Factorization of 28:
28 = 2 x 2 x 7 = 2² x 7
Prime Factorization of 24:
24 = 2 x 2 x 2 x 3 = 2³ x 3
Now, identify the common prime factors and their lowest powers:
Both 28 and 24 share the prime factor 2. The lowest power of 2 present in both factorizations is 2². There are no other common prime factors.
Therefore, the GCF is 2² = 4.
Therefore, the GCF of 28 and 24 is 4.
Finding the GCF of 28 and 24: Method 3 - Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply it to 28 and 24:
- Step 1: 28 - 24 = 4
- Step 2: Now find the GCF of 24 and 4.
- Step 3: 24 - (4 x 6) = 0
Since we've reached 0, the GCF is the last non-zero remainder, which is 4.
Therefore, the GCF of 28 and 24 is 4.
Applications of GCF in Real-World Scenarios
Understanding GCF extends beyond simple arithmetic exercises. It has practical applications in various fields:
-
Simplifying Fractions: Finding the GCF allows you to simplify fractions to their lowest terms. For example, the fraction 24/28 can be simplified to 6/7 by dividing both numerator and denominator by their GCF (4).
-
Geometry Problems: GCF is used in solving geometry problems involving dividing shapes into smaller, equal parts. For instance, determining the largest square tiles that can perfectly cover a rectangular floor requires finding the GCF of the floor's dimensions.
-
Data Organization: In computer science, the GCF helps in optimizing data structures and algorithms. For example, in memory allocation or data partitioning.
-
Music Theory: Understanding GCF plays a crucial role in music theory when working with rhythms and creating harmonious musical pieces.
-
Project Management: When managing projects requiring equal resource distribution among teams, finding the GCF helps optimize resource utilization.
Expanding on the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For prime factorization, you would simply find the prime factorization of each number and then identify the common prime factors with the lowest powers. For the Euclidean algorithm, you would find the GCF of the first two numbers, and then find the GCF of that result and the third number, and so on.
Why Understanding GCF is Important
Mastering the concept of GCF provides a strong foundation in mathematics and has significant implications for various fields. It enhances problem-solving skills, facilitates efficient calculations, and contributes to a deeper understanding of number theory. It allows for simplification, optimization, and a more structured approach to various numerical problems.
Conclusion: The Power of the GCF
The GCF, seemingly a simple concept, is a powerful tool with far-reaching applications. We've demonstrated multiple methods to calculate the GCF of 28 and 24, highlighting the versatility and practicality of this fundamental mathematical concept. Whether you're simplifying fractions, solving geometry puzzles, or tackling more complex mathematical problems, understanding and applying the concept of GCF is essential for success. The ability to efficiently find the GCF empowers you to tackle more complex mathematical challenges with confidence and precision. Remember, the key is not just knowing what the GCF is, but also why and how to find it effectively, choosing the most appropriate method for the task at hand.
Latest Posts
Latest Posts
-
What Part Of The Cow Does The T Bone Come From
Mar 29, 2025
-
What Is A Factor In An Experiment
Mar 29, 2025
-
What Is 34 In A Fraction
Mar 29, 2025
-
Is 6 8 Equivalent To 3 4
Mar 29, 2025
-
Whats 1 2 Of 1 3
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 28 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
