What Is The Gcf Of 27 And 45
listenit
Apr 01, 2025 · 5 min read
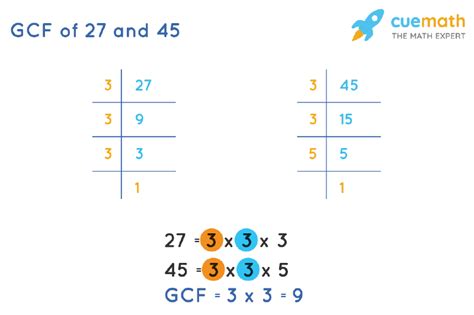
Table of Contents
What is the GCF of 27 and 45? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and exploring different methods can significantly enhance your mathematical skills and problem-solving abilities. This comprehensive guide delves into the question, "What is the GCF of 27 and 45?", exploring various techniques to determine the answer and expanding on the broader concept of GCFs.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the given integers without leaving a remainder. It's a fundamental concept in number theory with applications in various areas of mathematics and beyond. Think of it as the biggest number that perfectly fits into both numbers without any leftovers.
Why is finding the GCF important?
Understanding GCFs is crucial for various mathematical operations and real-world applications, including:
- Simplifying fractions: Finding the GCF of the numerator and denominator allows you to simplify fractions to their lowest terms.
- Solving algebraic equations: GCFs are often used to factor polynomials, a critical step in solving many algebraic equations.
- Geometry and Measurement: GCFs help in solving problems related to areas, volumes, and finding common measurements.
- Number theory: GCF is a fundamental concept in advanced number theory.
Methods for Finding the GCF of 27 and 45
Let's explore several methods to find the GCF of 27 and 45.
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
Factors of 27: 1, 3, 9, 27 Factors of 45: 1, 3, 5, 9, 15, 45
Comparing the two lists, we see that the common factors are 1, 3, and 9. The greatest of these is 9. Therefore, the GCF of 27 and 45 is 9.
This method is straightforward for smaller numbers but can become cumbersome with larger numbers.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime factorization of 27: 3 x 3 x 3 = 3³ Prime factorization of 45: 3 x 3 x 5 = 3² x 5
The common prime factor is 3. The lowest power of 3 present in both factorizations is 3². Therefore, the GCF is 3² = 9.
This method is more efficient for larger numbers than the listing factors method. It provides a systematic approach to finding the GCF.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially for larger numbers. It uses repeated division until the remainder is zero.
The steps are as follows:
-
Divide the larger number (45) by the smaller number (27). 45 ÷ 27 = 1 with a remainder of 18.
-
Replace the larger number with the smaller number (27) and the smaller number with the remainder (18). 27 ÷ 18 = 1 with a remainder of 9.
-
Repeat the process: 18 ÷ 9 = 2 with a remainder of 0.
When the remainder is 0, the GCF is the last non-zero remainder. In this case, the GCF is 9.
The Euclidean algorithm is highly efficient and is often preferred for finding the GCF of larger numbers. It's a cornerstone algorithm in number theory.
Expanding on the Concept of GCF
The concept of GCF extends beyond just finding the greatest common factor of two numbers. Here are some related concepts:
-
Least Common Multiple (LCM): The LCM is the smallest positive integer that is a multiple of each of the given integers. The relationship between GCF and LCM is given by the formula: GCF(a, b) x LCM(a, b) = a x b. For 27 and 45, the LCM is 135.
-
GCF of more than two numbers: The method of prime factorization can be easily extended to find the GCF of more than two numbers. You find the prime factorization of each number and identify the common prime factors raised to the lowest power.
-
GCF and Fractions: Understanding GCF is essential for simplifying fractions to their lowest terms. By dividing both the numerator and denominator by their GCF, you obtain an equivalent fraction in its simplest form. For example, the fraction 27/45 simplifies to 3/5 after dividing both the numerator and denominator by their GCF, 9.
-
GCF and Algebra: GCF plays a vital role in factoring algebraic expressions. Factoring involves expressing an algebraic expression as a product of simpler expressions. Finding the GCF of the terms in an expression allows you to factor out the common factor.
Real-world Applications of GCF
The seemingly abstract concept of GCF has numerous practical applications in various fields:
- Construction and Engineering: Determining the largest common dimension for cutting materials efficiently.
- Packaging and Logistics: Finding the optimal dimensions for packaging goods to minimize waste and maximize space.
- Computer Science: Used in algorithms for data compression, cryptography, and other computational tasks.
- Music Theory: Understanding GCF aids in analyzing musical harmonies and intervals.
Conclusion: Mastering the GCF
Finding the greatest common factor of 27 and 45, which is 9, is not merely an exercise in arithmetic but a stepping stone to understanding broader mathematical concepts. Whether you utilize the listing factors method, prime factorization, or the Euclidean algorithm, the key is understanding the underlying principles and selecting the most efficient approach based on the numbers involved. Mastering GCFs improves your problem-solving skills and opens doors to more complex mathematical concepts, demonstrating its importance beyond the classroom. The versatility of GCF extends far beyond basic arithmetic, offering practical applications in diverse fields, highlighting its significance in both theoretical and practical domains. So, next time you encounter a problem involving GCF, remember the various methods at your disposal and the vast applications this seemingly simple concept offers.
Latest Posts
Latest Posts
-
How Long Does It Take To Get To The Venus
Apr 02, 2025
-
03 Miles Is How Many Feet
Apr 02, 2025
-
Ions How Are Ions Made From Neutral Atoms
Apr 02, 2025
-
How Many Ounces Is 280 Grams
Apr 02, 2025
-
Compare The Sun And The Moon
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 27 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
