What Is The Gcf Of 10 And 12
listenit
Mar 27, 2025 · 5 min read
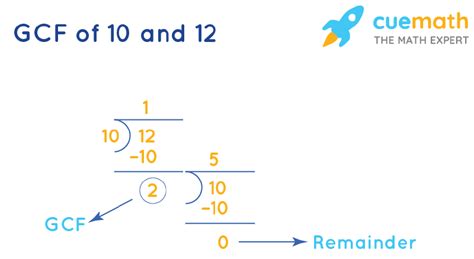
Table of Contents
What is the GCF of 10 and 12? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods to solve it unlocks a deeper understanding of number theory and its practical applications. This comprehensive guide will explore the GCF of 10 and 12, delving into multiple approaches to determine the answer, and exploring the broader significance of GCF in mathematics and beyond.
Understanding Greatest Common Factors (GCF)
Before we tackle the specific problem of finding the GCF of 10 and 12, let's establish a solid understanding of what a GCF is. The greatest common factor, also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers.
Identifying Factors
The foundation of finding the GCF lies in identifying the factors of each number. Factors are the numbers that divide a given number without leaving a remainder. For instance:
- Factors of 10: 1, 2, 5, 10
- Factors of 12: 1, 2, 3, 4, 6, 12
By listing the factors, we can visually compare them to identify the common factors.
Methods for Finding the GCF of 10 and 12
Several methods exist for determining the GCF, each offering unique insights and varying levels of efficiency. Let's explore the most common approaches:
1. Listing Factors Method
This is the most straightforward approach, especially for smaller numbers like 10 and 12. We've already listed the factors:
- Factors of 10: 1, 2, 5, 10
- Factors of 12: 1, 2, 3, 4, 6, 12
By comparing the two lists, we identify the common factors: 1 and 2. The greatest of these common factors is 2. Therefore, the GCF of 10 and 12 is 2.
2. Prime Factorization Method
This method involves expressing each number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that have only two divisors: 1 and themselves (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 10: 2 x 5
- Prime factorization of 12: 2 x 2 x 3 (or 2² x 3)
Now, we identify the common prime factors. Both 10 and 12 share one factor of 2. To find the GCF, we multiply the common prime factors: 2. Thus, the GCF of 10 and 12 is 2.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, particularly useful for larger numbers. It's based on repeated application of the division algorithm.
- Divide the larger number (12) by the smaller number (10): 12 ÷ 10 = 1 with a remainder of 2.
- Replace the larger number with the smaller number (10) and the smaller number with the remainder (2): Now we find the GCF of 10 and 2.
- Repeat the division: 10 ÷ 2 = 5 with a remainder of 0.
- The GCF is the last non-zero remainder. In this case, the last non-zero remainder is 2. Therefore, the GCF of 10 and 12 is 2.
Practical Applications of GCF
The concept of GCF extends far beyond simple arithmetic exercises. It finds practical applications in various fields:
1. Simplifying Fractions
GCF plays a crucial role in simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their GCF. For example, if we have the fraction 12/10, we find the GCF (which is 2), and simplify the fraction to 6/5.
2. Geometry and Measurement
GCF is essential in solving problems involving geometric shapes and measurements. For instance, when dividing a rectangular area into smaller, equally sized squares, the side length of the squares must be a common factor of the rectangle's length and width. The largest possible square size will be determined by the GCF.
3. Data Organization and Scheduling
In scenarios involving data organization or scheduling tasks, GCF helps find common patterns or cycles. For example, if two machines complete cycles every 10 and 12 minutes respectively, they will both be at the start of their cycles again after the least common multiple (LCM), which is closely related to the GCF.
4. Cryptography and Number Theory
GCF is a fundamental concept in number theory and plays a crucial role in cryptography, particularly in algorithms related to public-key cryptography.
Expanding the Concept: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). The LCM is the smallest positive integer that is a multiple of each of the integers. While we've focused on GCF here, understanding the relationship between GCF and LCM is important:
The product of the GCF and LCM of two numbers is always equal to the product of the two numbers. Therefore, once you know the GCF, you can easily calculate the LCM. For 10 and 12:
- GCF(10, 12) = 2
- LCM(10, 12) = (10 x 12) / 2 = 60
Conclusion: Mastering GCF
Finding the greatest common factor of 10 and 12, as demonstrated through various methods, is a stepping stone to understanding more complex number theory concepts. Whether using the simple listing method, the elegant prime factorization, or the efficient Euclidean algorithm, mastering GCF provides a solid foundation for tackling more challenging mathematical problems and solving practical real-world applications across diverse fields. The understanding of GCF is not just about finding a single answer but about grasping the underlying principles of number theory and its significance in various branches of mathematics and beyond. This deep dive into GCF provides a solid base for further exploration of more advanced mathematical concepts.
Latest Posts
Latest Posts
-
How Many Chromosomes Do Daughter Cells Have After Mitosis
Mar 30, 2025
-
Is Hydrobromic Acid A Strong Acid
Mar 30, 2025
-
Groups 3 12 On The Periodic Table
Mar 30, 2025
-
Lewis Structure Of N Ch3 3
Mar 30, 2025
-
What Is The Name For The Compound N2o5
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 10 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
