What Is The Equivalent Fraction For 7/8
listenit
Apr 01, 2025 · 6 min read
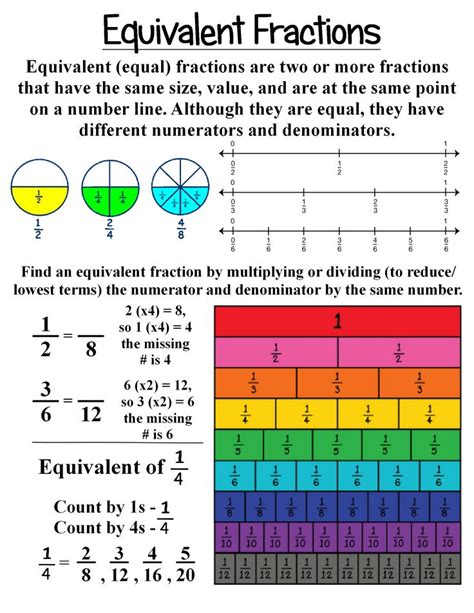
Table of Contents
What is the Equivalent Fraction for 7/8? A Deep Dive into Fraction Equivalence
Finding equivalent fractions might seem like a simple task, especially when dealing with a straightforward fraction like 7/8. However, understanding the underlying principles of fraction equivalence is crucial for a solid grasp of mathematical concepts and problem-solving. This comprehensive guide will not only answer the question, "What is the equivalent fraction for 7/8?" but also delve into the broader topic of fraction equivalence, providing you with the tools to tackle any equivalent fraction challenge with confidence.
Understanding Fractions: A Quick Recap
Before diving into the specifics of 7/8, let's briefly review the fundamental components of a fraction:
- Numerator: The top number in a fraction, representing the number of parts you have.
- Denominator: The bottom number in a fraction, representing the total number of equal parts in a whole.
A fraction, therefore, expresses a part of a whole. For example, in the fraction 7/8, the numerator (7) indicates that we have 7 parts, and the denominator (8) indicates that the whole is divided into 8 equal parts.
Finding Equivalent Fractions: The Core Principle
The key to finding equivalent fractions lies in the concept of proportionality. Equivalent fractions represent the same proportion or value, even though they appear different. This is achieved by multiplying or dividing both the numerator and the denominator by the same non-zero number. This process maintains the ratio between the numerator and the denominator, ensuring the value remains unchanged.
Think of it like this: Imagine a pizza cut into 8 slices. If you eat 7 slices, you've eaten 7/8 of the pizza. Now imagine the same pizza, but this time it's cut into 16 slices. If you eat 14 slices (twice the number of slices in the first scenario), you've still eaten the same proportion of the pizza – 14/16. Both 7/8 and 14/16 are equivalent fractions.
Determining Equivalent Fractions for 7/8
Let's apply the principle of proportionality to find equivalent fractions for 7/8. We can achieve this by multiplying both the numerator and the denominator by the same whole number:
- Multiplying by 2: (7 x 2) / (8 x 2) = 14/16
- Multiplying by 3: (7 x 3) / (8 x 3) = 21/24
- Multiplying by 4: (7 x 4) / (8 x 4) = 28/32
- Multiplying by 5: (7 x 5) / (8 x 5) = 35/40
- Multiplying by 6: (7 x 6) / (8 x 6) = 42/48
- Multiplying by 10: (7 x 10) / (8 x 10) = 70/80
- And so on...
You can continue this process indefinitely, generating an infinite number of equivalent fractions for 7/8. Each fraction will represent the same proportion, but with different numerators and denominators.
Simplifying Fractions: The Reverse Process
The reverse process of finding equivalent fractions is simplifying or reducing a fraction to its simplest form. This involves dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
For example, let's consider the equivalent fraction 14/16. The GCD of 14 and 16 is 2. Dividing both the numerator and denominator by 2 gives us:
(14 ÷ 2) / (16 ÷ 2) = 7/8
This demonstrates that 14/16 simplifies to 7/8, confirming their equivalence. 7/8 is considered the simplest form of the fraction because the numerator and denominator have no common divisors other than 1.
The Importance of Equivalent Fractions
Understanding equivalent fractions is crucial for several reasons:
-
Comparison: Equivalent fractions allow us to compare fractions with different denominators. For example, comparing 7/8 and 3/4 becomes easier when we express 3/4 as its equivalent fraction 6/8. We can then easily see that 7/8 is greater than 6/8.
-
Addition and Subtraction: Adding and subtracting fractions requires them to have the same denominator. Finding equivalent fractions allows us to manipulate fractions to have a common denominator, enabling straightforward addition or subtraction.
-
Problem Solving: Numerous real-world problems involve fractions, and understanding equivalent fractions is crucial for accurate problem-solving in various fields like cooking, construction, and engineering.
-
Decimal Conversion: Equivalent fractions play a critical role in converting fractions into decimals and vice versa. For example, finding an equivalent fraction with a denominator that is a power of 10 (like 10, 100, 1000) simplifies the conversion process. Consider 7/8. While directly converting is possible, finding an equivalent fraction like 875/1000 (by multiplying numerator and denominator by 125) makes the conversion to the decimal 0.875 much more straightforward.
Visualizing Equivalent Fractions
Visual aids can significantly help in understanding equivalent fractions. Imagine a rectangular bar representing a whole. Dividing the bar into 8 equal parts and shading 7 of them visually represents 7/8. You can then divide the same bar into 16 equal parts, and shading 14 parts will demonstrate the equivalence of 14/16 to 7/8. This visual representation reinforces the concept of maintaining the same proportion despite altering the number of parts.
Equivalent Fractions and Real-World Applications
The concept of equivalent fractions isn't confined to textbooks. It's integral to numerous everyday scenarios:
-
Cooking: Recipes often require fractions of ingredients. Understanding equivalent fractions is crucial for adjusting recipes based on the number of servings. If a recipe calls for 3/4 cup of sugar and you want to double the recipe, you need to know that 3/4 is equivalent to 6/8 or 1 1/2 cups.
-
Construction: Measuring and cutting materials in construction projects often involves fractions. Workers need to accurately determine the correct amount of materials using equivalent fractions.
-
Sewing: Patterns and measurements in sewing often utilize fractions. Understanding equivalent fractions helps ensure accurate cutting and assembly.
-
Finance: Calculating portions of investments, budgeting, or debt often requires using fractions and understanding their equivalence to make informed financial decisions.
Beyond 7/8: Mastering Fraction Equivalence
The principles discussed in relation to 7/8 are universally applicable to any fraction. The process of multiplying or dividing both the numerator and the denominator by the same non-zero number remains consistent regardless of the specific fraction. Practice with different fractions will solidify your understanding and improve your proficiency in manipulating and comparing fractions.
Conclusion: A Foundation for Further Mathematical Exploration
Understanding the concept of equivalent fractions for 7/8, and more broadly, for all fractions, is a fundamental building block in mathematics. Mastering this concept opens doors to more advanced mathematical concepts, including ratios, proportions, percentages, and algebraic manipulations. The ability to confidently work with fractions is a valuable skill with widespread applications in various fields and everyday life. Therefore, dedicating time to mastering this concept is an investment in your overall mathematical proficiency and problem-solving abilities. So, go forth and conquer the world of fractions!
Latest Posts
Latest Posts
-
24 To The Power Of 2
Apr 02, 2025
-
Lowest Common Multiple Of 14 And 35
Apr 02, 2025
-
What Is The Limit Of A Constant
Apr 02, 2025
-
X 3 2x 2 X 2 0
Apr 02, 2025
-
1 3 Divided By 1 6 As A Fraction
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Equivalent Fraction For 7/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
