1 3 Divided By 1 6 As A Fraction
listenit
Apr 02, 2025 · 4 min read
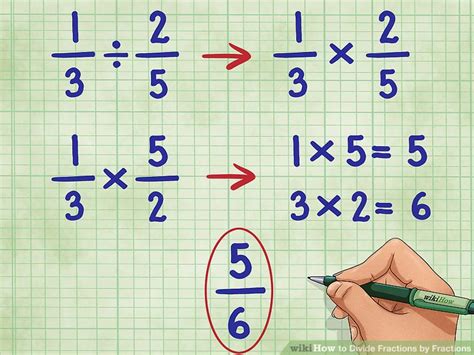
Table of Contents
1 ⅓ Divided by 1 ⁶⁄₁₀ as a Fraction: A Comprehensive Guide
Understanding division with mixed numbers can sometimes feel tricky, but breaking it down into manageable steps reveals a straightforward process. This article will explore how to solve the problem "1 ⅓ divided by 1 ⁶⁄₁₀ as a fraction," providing a clear, step-by-step explanation, along with helpful tips and examples to solidify your understanding of fraction division. We'll also delve into the underlying mathematical concepts and explore different approaches to tackle similar problems.
Converting Mixed Numbers to Improper Fractions
Before we tackle the division, the first crucial step is converting our mixed numbers (numbers with both a whole number and a fraction) into improper fractions (fractions where the numerator is larger than the denominator). This makes the division process much simpler.
What are Mixed Numbers and Improper Fractions?
-
Mixed Numbers: These combine a whole number and a fraction, such as 1 ⅓ or 2 ¾. They represent a value greater than one.
-
Improper Fractions: In these fractions, the numerator (top number) is larger than or equal to the denominator (bottom number). Examples include ⁴⁄₃ and ¹¹⁄₄.
Converting 1 ⅓ to an Improper Fraction
- Multiply the whole number by the denominator: 1 x 3 = 3
- Add the numerator: 3 + 1 = 4
- Keep the same denominator: 3
Therefore, 1 ⅓ is equal to ⁴⁄₃.
Converting 1 ⁶⁄₁₀ to an Improper Fraction
- Multiply the whole number by the denominator: 1 x 10 = 10
- Add the numerator: 10 + 6 = 16
- Keep the same denominator: 10
Therefore, 1 ⁶⁄₁₀ is equal to ¹⁶⁄₁₀.
Dividing Fractions: The Reciprocal Method
Now that we've converted our mixed numbers into improper fractions, we can move on to the division. The most efficient method for dividing fractions involves using reciprocals.
What is a Reciprocal?
A reciprocal of a fraction is simply the fraction flipped upside down. To find the reciprocal, you swap the numerator and the denominator. For example:
- The reciprocal of ⁴⁄₃ is ³⁄₄.
- The reciprocal of ¹⁶⁄₁₀ is ¹⁰⁄₁₆.
Performing the Division
Dividing by a fraction is the same as multiplying by its reciprocal. Therefore, our problem becomes:
⁴⁄₃ ÷ ¹⁶⁄₁₀ = ⁴⁄₃ x ¹⁰⁄₁₆
Simplifying Before Multiplication
Before we multiply the numerators and denominators, we can simplify the fractions to make the calculation easier. This is done by finding common factors between the numerators and denominators and canceling them out.
Notice that:
- 4 and 16 share a common factor of 4 (4 ÷ 4 = 1 and 16 ÷ 4 = 4).
- 3 and 10 do not share a common factor.
Therefore, we simplify our equation:
(⁴⁄₃) x (¹⁰⁄₁₆) = (¹⁄₃) x (¹⁰⁄₄)
Now we can simplify further:
(¹⁄₃) x (¹⁰⁄₄) = (¹⁄₃) x (⁵⁄₂)
Completing the Multiplication
Now, we multiply the numerators together and the denominators together:
(¹⁄₃) x (⁵⁄₂) = ⁵⁄₆
Therefore, 1 ⅓ divided by 1 ⁶⁄₁₀ is equal to ⁵⁄₆.
Alternative Approaches: Using Decimal Representation
While the reciprocal method is generally preferred for fraction division, we can also explore solving the problem using decimal representations.
-
Convert the mixed numbers to decimals:
- 1 ⅓ = 1.333... (recurring decimal)
- 1 ⁶⁄₁₀ = 1.6
-
Perform the decimal division: 1.333... ÷ 1.6 ≈ 0.833...
-
Convert the decimal back to a fraction: This step requires some understanding of recurring decimals and fraction conversion. The approximate decimal 0.833... is close to ⁵⁄₆.
This method is less precise, particularly with recurring decimals, and the fraction conversion back from a decimal can be more complex. Therefore, the reciprocal method is generally more accurate and efficient.
Real-World Applications and Further Exploration
Understanding fraction division extends beyond the realm of abstract mathematics; it finds practical applications in various real-world scenarios:
-
Baking and Cooking: Recipes often require precise measurements, and adjusting ingredient quantities involves fraction division. For example, if a recipe calls for a specific amount of flour and you need to halve the recipe, you'll be using fraction division.
-
Sewing and Crafting: Many craft projects involve cutting fabric or other materials into specific sizes. If you need to divide a length of fabric into equal parts, you'll use fraction division.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering projects. Dividing lengths, volumes, or areas often requires working with fractions.
-
Data Analysis and Statistics: When working with data that includes fractions or percentages, you may need to divide fractions to understand relationships or proportions.
Troubleshooting and Common Mistakes
-
Forgetting to convert mixed numbers to improper fractions: This is the most common mistake. Remember that you must convert mixed numbers to improper fractions before performing the division.
-
Incorrectly applying the reciprocal: Ensure you are flipping the divisor (the second fraction) and not the dividend (the first fraction).
-
Not simplifying before multiplication: Simplifying fractions before multiplication significantly reduces the complexity of the calculation and minimizes the risk of errors.
-
Errors in multiplication: Double-check your multiplication of numerators and denominators to ensure accuracy.
Conclusion
Mastering fraction division, especially with mixed numbers, is a valuable skill with far-reaching applications. By carefully following the steps outlined in this guide, converting mixed numbers to improper fractions, using the reciprocal method, and simplifying along the way, you can confidently solve problems involving fraction division. Remember to practice regularly to build fluency and accuracy. The more you practice, the more comfortable and proficient you will become in handling these types of calculations. By understanding the underlying mathematical principles and the practical applications of fraction division, you are building a solid foundation for success in various mathematical and real-world contexts.
Latest Posts
Latest Posts
-
How Many Fluid Ounces In A Fifth
Apr 03, 2025
-
How Much 70 Fahrenheit In Celsius
Apr 03, 2025
-
All Living Things Are Made Of What
Apr 03, 2025
-
The Movement Of Water Through A Selectively Permeable Membrane
Apr 03, 2025
-
What Percent Is 3 Out Of 20
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Divided By 1 6 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
