What Is The Difference Between A Rhombus And Parallelogram
listenit
Apr 05, 2025 · 5 min read
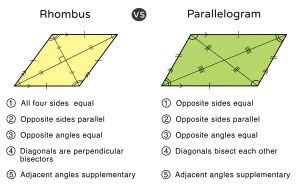
Table of Contents
What's the Difference Between a Rhombus and a Parallelogram? A Deep Dive into Quadrilaterals
Understanding the differences between geometric shapes can sometimes feel like navigating a maze. Two shapes that often cause confusion are the rhombus and the parallelogram. While closely related, they possess distinct characteristics that set them apart. This comprehensive guide will delve into the intricacies of both shapes, clarifying their similarities and highlighting their crucial differences. We'll explore their properties, formulas, and even touch upon real-world applications. By the end, you'll be able to confidently distinguish a rhombus from a parallelogram and appreciate the beauty of geometric precision.
Defining the Parallelogram
A parallelogram is a quadrilateral – a closed two-dimensional shape with four sides – defined by a very specific set of properties:
- Opposite sides are parallel: This is the fundamental defining characteristic. Two pairs of opposite sides run in the same direction and will never intersect, no matter how far they're extended.
- Opposite sides are equal in length: The lengths of opposite sides are always congruent (equal).
- Opposite angles are equal in measure: The angles opposite each other within the parallelogram are always the same size.
- Consecutive angles are supplementary: Any two angles that share a side add up to 180 degrees.
These properties are interconnected; if you know that opposite sides are parallel, you automatically know they are also equal in length. The same interconnectedness applies to the angles. This interconnectedness makes parallelograms remarkably stable and predictable geometric forms.
Types of Parallelograms
It's important to remember that the parallelogram is a broader category encompassing several other specific quadrilaterals. These include:
- Rectangles: Parallelograms with four right angles (90-degree angles).
- Squares: Rectangles with four sides of equal length.
- Rhombuses: Parallelograms with four sides of equal length (this is where our focus shifts).
Defining the Rhombus
A rhombus, often called a diamond, is a special type of parallelogram. This means it inherits all the properties of a parallelogram (parallel and equal opposite sides, equal opposite angles, supplementary consecutive angles). However, a rhombus adds a crucial defining characteristic:
- All four sides are equal in length: This is the key differentiator between a rhombus and a general parallelogram. While a parallelogram only requires opposite sides to be equal, a rhombus mandates that all sides are congruent.
Because a rhombus is a parallelogram, it automatically possesses all the parallelogram properties listed above. This makes it a more specialized and restricted shape.
Key Differences Summarized: Parallelogram vs. Rhombus
The table below neatly summarizes the crucial differences between a parallelogram and a rhombus:
| Feature | Parallelogram | Rhombus |
|---|---|---|
| Side Lengths | Opposite sides are equal in length | All four sides are equal in length |
| Angles | Opposite angles are equal; consecutive angles are supplementary | Opposite angles are equal; consecutive angles are supplementary |
| Parallel Sides | Opposite sides are parallel | Opposite sides are parallel |
| Relationship | General quadrilateral; broader category | Special type of parallelogram; more specific |
Exploring the Properties Further: Area and Perimeter
Both parallelograms and rhombuses have easily calculated areas and perimeters:
Parallelogram:
- Perimeter: P = 2(a + b), where 'a' and 'b' are the lengths of adjacent sides.
- Area: A = b * h, where 'b' is the length of the base and 'h' is the perpendicular height.
Rhombus:
- Perimeter: P = 4a, where 'a' is the length of one side (since all sides are equal).
- Area: A = (d1 * d2) / 2, where 'd1' and 'd2' are the lengths of the diagonals. Alternatively, A = b * h, where 'b' is the length of a side and 'h' is the perpendicular height.
The area formula using diagonals is unique to the rhombus because of its symmetrical nature. The diagonals of a rhombus are perpendicular bisectors of each other (they intersect at a 90-degree angle and divide each other into two equal parts). This property isn't guaranteed in a general parallelogram.
Real-world Examples and Applications
Understanding the differences between parallelograms and rhombuses extends beyond theoretical geometry. These shapes appear frequently in the real world:
-
Parallelograms: Think of windows, doors, tabletops, and even the faces of some buildings. The stability offered by parallel sides makes them ideal for construction and design.
-
Rhombuses: The classic example is a diamond shape. You'll find rhombuses in various designs, from artwork and logos to the crystalline structures of certain minerals. The strength and symmetry of a rhombus make it suitable for reinforcement in some engineering applications.
Beyond the Basics: Advanced Concepts
For those seeking a deeper understanding, let's explore some more advanced concepts:
Vectors and Parallelograms
Parallelograms are fundamentally linked to vector addition. If you consider two vectors originating from a single point, the parallelogram formed by these vectors represents the resultant vector obtained by adding the two individual vectors.
Tessellations and Rhombuses
Rhombuses can be used to create interesting and complex tessellations (patterns that cover a surface without overlaps or gaps). The symmetry of a rhombus makes it particularly well-suited for this purpose. Think of honeycomb structures; while not perfect rhombuses, they closely approximate the shape and demonstrate the tessellation principle.
Conclusion: Mastering the Shapes
The distinctions between parallelograms and rhombuses may seem subtle at first, but grasping these differences unlocks a deeper understanding of geometry and its applications. A rhombus is a specialized parallelogram, inheriting all the properties of a parallelogram and adding the unique characteristic of equal side lengths. Remembering these defining features, along with their area and perimeter formulas, will equip you to confidently identify and analyze these shapes in various contexts – from mathematical problems to real-world observations. The journey into geometry is a continuous exploration, and understanding these fundamental shapes is a crucial step in that adventure. So, next time you encounter a parallelogram or a rhombus, you'll be able to appreciate their unique characteristics and the mathematical elegance they embody.
Latest Posts
Latest Posts
-
How To Cite The Epic Of Gilgamesh
Apr 05, 2025
-
Lcm Of 4 9 And 12
Apr 05, 2025
-
3 Class Of Levers With Examples
Apr 05, 2025
-
What Does A Negative Acceleration Mean
Apr 05, 2025
-
During A Chemical Reaction Atoms Are
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The Difference Between A Rhombus And Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
