What Is The Decimal For 7 9
listenit
Apr 03, 2025 · 5 min read
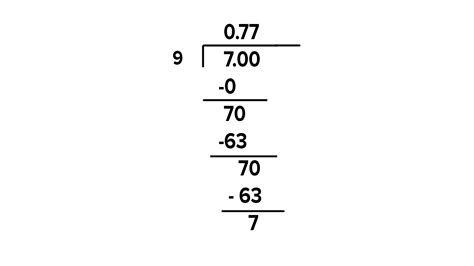
Table of Contents
What is the Decimal for 7/9? A Deep Dive into Decimal Conversions and Their Applications
The question "What is the decimal for 7/9?" seems deceptively simple. However, exploring this seemingly straightforward fraction opens a door to a fascinating world of decimal representations, repeating decimals, and their practical applications across various fields. This article will not only answer the initial question but will delve into the underlying mathematical concepts and illustrate the importance of understanding decimal conversions.
Understanding Fractions and Decimals
Before we tackle 7/9, let's establish a firm grasp of the relationship between fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two integers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). The decimal point separates the whole number part from the fractional part.
Converting a fraction to a decimal involves dividing the numerator by the denominator. This process sometimes yields a terminating decimal, meaning the decimal representation ends after a finite number of digits (e.g., 1/4 = 0.25). Other times, the division results in a repeating decimal (or recurring decimal), where a sequence of digits repeats indefinitely (e.g., 1/3 = 0.333...).
Calculating the Decimal for 7/9
Now, let's address the central question: what is the decimal representation of 7/9? To find out, we perform the division: 7 ÷ 9.
Performing long division, we get:
0.7777...
9 | 7.0000
6.3
0.70
0.63
0.070
0.063
0.0070
0.0063
...
As you can see, the digit 7 repeats infinitely. Therefore, the decimal representation of 7/9 is 0.7̅ (where the bar above the 7 indicates the repeating digit).
Understanding Repeating Decimals
The repeating nature of the decimal for 7/9 is not a coincidence. It's a characteristic of fractions where the denominator, when simplified to its lowest terms, contains prime factors other than 2 and 5. Since 9 = 3 x 3, it contains a prime factor (3) other than 2 and 5, leading to a repeating decimal. Fractions with denominators that are only composed of 2s and 5s (or powers of 2 and 5) will always produce terminating decimals.
Different Representations of Repeating Decimals
There are several ways to represent repeating decimals:
- Using a bar: This is the most common method, as shown above: 0.7̅.
- Using ellipses: This shows the continuation of the repeating pattern: 0.777...
- Using parentheses: Some texts use parentheses to enclose the repeating block: 0.(7)
All three methods indicate the same value—an infinite repetition of the digit 7.
Applications of Decimal Conversions
The ability to convert fractions to decimals (and vice versa) is crucial in various fields:
-
Engineering and Physics: Accurate calculations in these fields often require decimal precision. Converting fractions to decimals allows for easier computation and analysis. For example, calculating the precise dimensions of a component or determining the exact speed of an object may necessitate the use of decimals.
-
Finance: Dealing with money frequently involves decimal calculations. Converting fractional shares or calculating interest often requires the precision that decimal numbers offer. Imagine calculating profits or losses, or determining interest rates without the capability to use decimals. It would make financial transactions substantially harder and less precise.
-
Computer Science: While computers work with binary (base-2) systems, understanding decimal representations is essential for programmers to translate between human-readable numbers and machine-readable data. Converting between fractional representations and decimal systems is key to many algorithms, software, and applications.
-
Measurement and Statistics: Many measurements use decimal systems. Analyzing data, performing calculations related to averages, standard deviations, and other statistical concepts often involves decimal computations. The seamless integration of decimals into everyday measurements and statistics calculations greatly improves the efficiency and accuracy of the data analysis process.
-
Everyday Life: From calculating tips in restaurants to measuring ingredients in recipes, decimal representations are an integral part of our daily lives. The ease and efficiency of using decimals in daily tasks make them a cornerstone of practical mathematics.
Beyond 7/9: Exploring Other Fractions
Understanding the decimal representation of 7/9 allows us to generalize our understanding to other fractions. Let's explore a few more examples:
-
1/3 = 0.3̅: Similar to 7/9, this fraction also results in a repeating decimal.
-
1/7 = 0.142857̅: This fraction has a repeating block of six digits.
-
5/6 = 0.83̅: This fraction demonstrates how different fractions can have different repeating patterns.
By understanding how these conversions work, we gain a deeper appreciation of the interconnectedness of fractions and decimals within the broader field of mathematics.
Conclusion: The Significance of Decimal Conversions
The simple question of "What is the decimal for 7/9?" leads to a richer understanding of fundamental mathematical concepts. Mastering decimal conversions empowers us to solve problems across diverse fields, highlighting the significance of seemingly basic mathematical skills in our increasingly data-driven world. From the intricate calculations of engineers to the everyday tasks of individuals, understanding fractions and decimals plays a crucial role in achieving precision, accuracy, and efficiency. Therefore, a solid grasp of these concepts remains a valuable asset in various aspects of life and work. Further exploration into different number systems and their inter-relationships would enrich our mathematical understanding even further. The beauty of mathematics lies in its interconnectedness, and the journey from a simple fraction to its decimal representation exemplifies this beautifully.
Latest Posts
Latest Posts
-
What Color Is The Coolest Star
Apr 04, 2025
-
How Many Valence Electrons Are In Mg
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Decimal For 7 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
