What Is An Acute Isosceles Triangle
listenit
Apr 05, 2025 · 6 min read
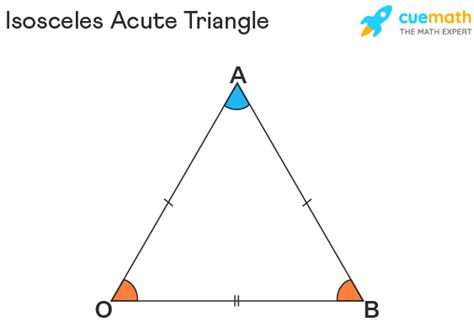
Table of Contents
What is an Acute Isosceles Triangle? A Deep Dive into Geometry
Understanding different types of triangles is fundamental in geometry. While many focus on right-angled triangles, the world of triangles extends far beyond this single category. Today, we'll delve deep into the fascinating world of acute isosceles triangles, exploring their properties, characteristics, and applications. By the end of this comprehensive guide, you'll have a solid grasp of this specific geometric shape and its significance in various mathematical contexts.
Defining the Acute Isosceles Triangle
Before we dive into the specifics, let's define the key terms:
-
Isosceles Triangle: An isosceles triangle is a triangle with at least two sides of equal length. These equal sides are called legs, and the angle formed between them is called the vertex angle. The third side is called the base.
-
Acute Triangle: An acute triangle is a triangle where all three interior angles are acute angles—meaning each angle measures less than 90 degrees.
Therefore, an acute isosceles triangle is a triangle that possesses both characteristics: it has two equal sides (making it isosceles) and all three angles are less than 90 degrees (making it acute).
Key Properties of Acute Isosceles Triangles
Acute isosceles triangles possess several unique properties stemming from their dual nature:
1. Equal Sides and Angles:
The most defining property is the presence of two equal sides. This directly impacts the angles opposite these sides. A fundamental theorem of geometry states that angles opposite equal sides in a triangle are equal. In an acute isosceles triangle, this means that the two angles opposite the equal sides are also equal.
2. Angle Sum:
Like all triangles, the sum of the interior angles of an acute isosceles triangle is always 180 degrees. This is a cornerstone principle of Euclidean geometry. Knowing this, and that two angles are equal, allows us to easily calculate the angles if we know one.
3. Angle Restrictions:
Because it's an acute isosceles triangle, each of its three angles must be less than 90 degrees. This limits the possible values of the angles. The vertex angle (the angle between the two equal sides) can range from slightly above zero to less than 90 degrees.
4. Altitude, Median, and Angle Bisector Coincidence:
In an isosceles triangle, the altitude (perpendicular line from the vertex angle to the base), the median (line segment from the vertex angle to the midpoint of the base), and the angle bisector (line that divides the vertex angle into two equal angles) are all concurrent. They all meet at the same point. This point is often referred to as the orthocenter, centroid, or incenter in more general triangle contexts. In an isosceles triangle, these three points coincide.
5. Area Calculation:
The area of any triangle can be calculated using the formula: Area = (1/2) * base * height. In an isosceles triangle, the height is the altitude from the vertex angle to the base. This height bisects the base, creating two smaller, congruent right-angled triangles.
Examples and Illustrations of Acute Isosceles Triangles
Let's consider a few examples to solidify our understanding:
Example 1: Imagine a triangle with sides of length 5 cm, 5 cm, and 6 cm. Since two sides are equal, it's isosceles. If we calculate the angles using the Law of Cosines, we find that all angles are less than 90 degrees, confirming its acute nature.
Example 2: Consider a triangle with angles of 70, 70, and 40 degrees. Since two angles are equal, the sides opposite those angles are also equal (by the converse of the theorem mentioned earlier), making it an isosceles triangle. Because all angles are less than 90 degrees, it's acute.
Example 3: An equilateral triangle is a special case of an acute isosceles triangle. An equilateral triangle has all three sides equal and all three angles equal to 60 degrees. Since all angles are acute, it fits the definition.
Differentiating Acute Isosceles Triangles from Other Triangles
It's crucial to differentiate acute isosceles triangles from other types of triangles:
-
Obtuse Isosceles Triangle: This triangle has two equal sides, but one angle is greater than 90 degrees.
-
Right Isosceles Triangle: This triangle has two equal sides, and one angle is exactly 90 degrees.
-
Scalene Triangle: A scalene triangle has no equal sides and no equal angles.
-
Acute Scalene Triangle: This triangle has all angles less than 90 degrees, but no sides are equal.
Understanding these distinctions is vital for accurate geometric problem-solving.
Applications of Acute Isosceles Triangles
Acute isosceles triangles appear frequently in various applications:
-
Architecture: Many architectural designs incorporate isosceles triangles, often for aesthetic or structural reasons. The acute variety might be found in roof structures or decorative elements.
-
Engineering: Structural engineers utilize geometric principles, including those related to acute isosceles triangles, in bridge construction, building design, and other projects requiring stability and strength.
-
Art and Design: The balanced and symmetrical nature of isosceles triangles lends itself to artistic expressions. Artists often use geometric shapes, including acute isosceles triangles, to create visually appealing designs and patterns.
Solving Problems Involving Acute Isosceles Triangles
Let's tackle a sample problem to demonstrate the practical application of our knowledge:
Problem: An acute isosceles triangle has a base of 10 cm and two equal sides of 8 cm each. Find the area of the triangle.
Solution:
-
Draw a diagram: Sketch an acute isosceles triangle with the given dimensions.
-
Find the height: Draw an altitude from the vertex angle to the midpoint of the base. This altitude divides the triangle into two congruent right-angled triangles. Each smaller triangle has a hypotenuse of 8 cm and one leg of 5 cm (half the base). We can use the Pythagorean theorem (a² + b² = c²) to find the height (h): h² + 5² = 8² => h² = 64 - 25 = 39 => h = √39 cm
-
Calculate the area: Using the area formula, Area = (1/2) * base * height = (1/2) * 10 cm * √39 cm ≈ 31.22 cm²
This example showcases how understanding the properties of acute isosceles triangles allows us to solve practical geometric problems.
Advanced Concepts and Further Exploration
For those interested in delving deeper, exploring more advanced concepts related to acute isosceles triangles can be rewarding. This could include:
-
Trigonometric functions: Applying trigonometric ratios (sine, cosine, tangent) to determine angles and side lengths within acute isosceles triangles.
-
Coordinate geometry: Representing acute isosceles triangles using coordinates in a Cartesian plane and using coordinate geometry techniques to analyze their properties.
-
Geometric proofs: Developing formal proofs to demonstrate various theorems related to acute isosceles triangles. This involves rigorous logical reasoning and understanding of geometric axioms and postulates.
Conclusion
Acute isosceles triangles are more than just a geometric abstraction. Their unique properties and predictable behavior make them essential components in various fields. From architectural designs to advanced mathematical proofs, understanding their characteristics is crucial for both practical applications and theoretical exploration. This in-depth guide provides a solid foundation for anyone seeking a deeper understanding of this fascinating geometric shape. By mastering the concepts outlined here, you'll be equipped to tackle more complex geometric problems and appreciate the elegance and utility of acute isosceles triangles in the broader context of mathematics and beyond. Remember to practice solving various problems to solidify your understanding and enhance your problem-solving skills.
Latest Posts
Latest Posts
-
Three Less Than Six Times A Number
Apr 06, 2025
-
Mass Of Hydrogen Atom In G
Apr 06, 2025
-
What Is 240 Inches In Feet
Apr 06, 2025
-
What Is An Isosceles Obtuse Triangle
Apr 06, 2025
-
Is Boiling Water Physical Or Chemical Change
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is An Acute Isosceles Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
