What Is An Isosceles Obtuse Triangle
listenit
Apr 06, 2025 · 6 min read
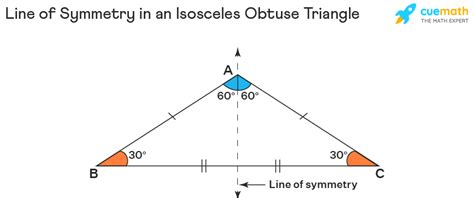
Table of Contents
What is an Isosceles Obtuse Triangle? A Deep Dive into Geometry
An isosceles obtuse triangle is a fascinating geometric shape that combines the properties of two seemingly contradictory types of triangles: isosceles and obtuse. Understanding its unique characteristics requires a grasp of fundamental geometric concepts. This comprehensive guide delves into the definition, properties, examples, and applications of isosceles obtuse triangles, aiming to provide a thorough understanding for both beginners and those seeking to refresh their knowledge.
Defining the Isosceles Obtuse Triangle
To understand an isosceles obtuse triangle, let's break down its defining features:
-
Isosceles Triangle: An isosceles triangle is a triangle with at least two sides of equal length. These equal sides are called legs, and the angle between them is called the vertex angle. The third side, which is potentially different in length, is called the base.
-
Obtuse Triangle: An obtuse triangle is a triangle with one obtuse angle (an angle greater than 90 degrees but less than 180 degrees). The other two angles must be acute angles (less than 90 degrees).
Therefore, an isosceles obtuse triangle is a triangle that possesses both characteristics:
- It has at least two sides of equal length (isosceles).
- It has one angle greater than 90 degrees (obtuse).
This combination of properties significantly limits the possible shapes and angles within the triangle. It's crucial to remember that only one angle can be obtuse; otherwise, the sum of the angles would exceed 180 degrees, violating the fundamental rule of triangle geometry.
Properties of Isosceles Obtuse Triangles
Several key properties uniquely define isosceles obtuse triangles:
-
Two Equal Sides and Angles: The two sides of equal length are opposite two angles of equal measure. This is a fundamental property of all isosceles triangles.
-
One Obtuse Angle: The triangle contains precisely one angle that measures greater than 90 degrees. This angle is always the angle between the two unequal sides.
-
Two Acute Angles: The remaining two angles are acute (less than 90 degrees). These acute angles are always equal to each other.
-
Angle Sum: Like all triangles, the sum of the interior angles of an isosceles obtuse triangle is always 180 degrees.
-
Altitude and Median: The altitude (perpendicular height) from the vertex angle to the base bisects both the base and the vertex angle. This creates two congruent right-angled triangles.
-
Circumcenter and Incenter: The circumcenter (the center of the circumscribed circle) and incenter (the center of the inscribed circle) lie outside the triangle. This is a unique property differentiating it from acute and right-angled isosceles triangles.
Understanding the Angle Restrictions
The obtuse angle in an isosceles obtuse triangle significantly restricts the possible values of the other angles. Because the sum of the angles must be 180 degrees, and two angles are equal, we can express the relationship algebraically. Let's denote the obtuse angle as 'x' and the two equal acute angles as 'y'. Then:
x + y + y = 180 degrees
This simplifies to:
x + 2y = 180 degrees
Since x must be greater than 90 degrees, and y must be less than 90 degrees, the possible range of values for x and y is limited. For example, if x = 100 degrees, then 2y = 80 degrees, meaning y = 40 degrees. If x = 120 degrees, then y = 30 degrees.
Examples of Isosceles Obtuse Triangles
While we can't draw perfect geometric representations here, let's visualize some scenarios:
-
Imagine a triangle with sides of length 5, 5, and 8. The two sides of length 5 are the equal sides. The angle opposite the longest side (length 8) will be the obtuse angle.
-
Consider a triangle with angles of 100, 40, and 40 degrees. This fits the definition; it has two equal angles (40 degrees) and one obtuse angle (100 degrees).
Applications of Isosceles Obtuse Triangles
While less commonly encountered in everyday applications compared to right-angled triangles, isosceles obtuse triangles appear in various contexts:
-
Architecture and Design: Certain architectural designs, particularly in roofs and decorative elements, might incorporate isosceles obtuse triangles. The unique shape provides structural stability and visual appeal.
-
Engineering: Structural engineering sometimes involves calculations related to forces and stresses within various shapes, including isosceles obtuse triangles.
-
Computer Graphics: The precise angles and side lengths are important in creating realistic 3D models and simulations in computer graphics.
-
Advanced Mathematics: Isosceles obtuse triangles play a role in various advanced geometric theorems and proofs. Their properties are crucial in solving complex geometric problems.
-
Cartography: Representations of land areas on maps sometimes utilise triangular approximations. Depending on the terrain, an isosceles obtuse triangle might be a suitable representation.
Distinguishing Isosceles Obtuse Triangles from Other Triangles
It’s crucial to differentiate an isosceles obtuse triangle from other triangle types:
-
Equilateral Triangles: All sides and angles are equal (60 degrees each). It cannot be obtuse.
-
Isosceles Acute Triangles: Two equal sides and all angles are acute (less than 90 degrees).
-
Isosceles Right Triangles: Two equal sides and one right angle (90 degrees).
-
Scalene Triangles: All sides and angles are unequal. A scalene triangle can be obtuse, acute, or right-angled.
-
Obtuse Triangles: One obtuse angle; the other two are acute. It could be isosceles or scalene.
Solving Problems Involving Isosceles Obtuse Triangles
Many problems related to isosceles obtuse triangles involve using trigonometric functions (sine, cosine, tangent) to find unknown sides or angles. Knowing the properties of the triangle is crucial in setting up the correct equations. Here's a general approach:
-
Identify the known information: What sides and angles are given?
-
Determine the unknown: What side lengths or angles do you need to find?
-
Apply relevant trigonometric functions or geometric theorems: Use the appropriate formula based on what you know. The sine rule, cosine rule, and Pythagoras' theorem (in the case of right-angled triangles formed by altitudes) are frequently employed.
-
Solve the equations: Use algebraic techniques to solve for the unknowns.
-
Check your solution: Ensure the calculated angles add up to 180 degrees and that the side lengths conform to the triangle inequality theorem (the sum of the lengths of any two sides must be greater than the length of the third side).
Conclusion: The Importance of Understanding Isosceles Obtuse Triangles
Isosceles obtuse triangles, while perhaps less frequently discussed than their right-angled counterparts, represent an important class of geometric shapes. Understanding their properties and characteristics is essential for anyone studying geometry or working in fields that require geometric analysis. From architectural design to advanced mathematical proofs, their unique combination of equal sides and an obtuse angle makes them a significant topic in geometry. By grasping the concepts outlined in this guide, you'll enhance your geometric understanding and improve your ability to tackle problems involving this specific type of triangle. Remember, the key is to practice and apply the principles learned to build a solid foundational knowledge.
Latest Posts
Latest Posts
-
What Is The Fraction Of 85
Apr 06, 2025
-
How Many Unpaired Electrons Does Mn Have
Apr 06, 2025
-
The Central Part Of The Atom Is Called The
Apr 06, 2025
-
Is The Number 13 Prime Or Composite
Apr 06, 2025
-
Suppose That Y Varies Directly With X
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is An Isosceles Obtuse Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
