What Is 8 Divided By 3 4
listenit
May 24, 2025 · 5 min read
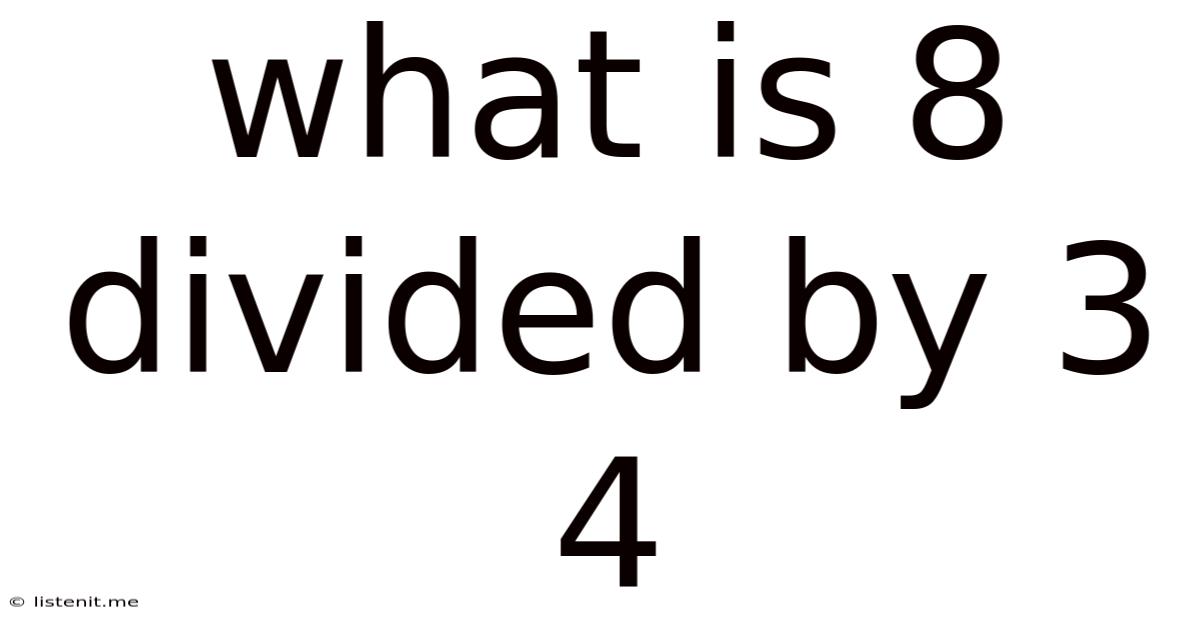
Table of Contents
What is 8 Divided by 3/4? A Comprehensive Guide to Fraction Division
Understanding fraction division can be tricky, but mastering it unlocks a world of mathematical possibilities. This comprehensive guide will walk you through the process of dividing 8 by 3/4, explaining the underlying concepts and providing you with various methods to solve this type of problem. We'll delve into the why, not just the how, ensuring a solid understanding that extends beyond this specific calculation.
Understanding the Problem: 8 ÷ 3/4
The question "What is 8 divided by 3/4?" asks us to determine how many times the fraction 3/4 fits into the whole number 8. This is a fundamental concept in fraction division—finding the number of times one quantity is contained within another. We'll explore several ways to solve this, emphasizing the importance of understanding the underlying principles.
Method 1: The "Keep, Change, Flip" Method
This is arguably the most popular method for dividing fractions, and it works perfectly well even when dividing a whole number by a fraction. The steps are as follows:
-
Keep: Keep the first number (the dividend) as it is. In our case, this remains 8.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip (or find the reciprocal of) the second number (the divisor). The reciprocal of 3/4 is 4/3.
Therefore, our problem transforms from 8 ÷ 3/4 to 8 × 4/3.
-
Multiply: Now, multiply the numerators (top numbers) together and the denominators (bottom numbers) together.
8 × 4 = 32 1 × 3 = 3
This gives us the improper fraction 32/3.
-
Convert to a Mixed Number (Optional): Improper fractions (where the numerator is larger than the denominator) are often converted to mixed numbers for easier interpretation. To do this, divide the numerator by the denominator:
32 ÷ 3 = 10 with a remainder of 2.
Therefore, 32/3 can be written as the mixed number 10 2/3.
Therefore, 8 divided by 3/4 is 10 2/3.
Method 2: Visual Representation
Let's visualize this division problem. Imagine you have 8 whole pizzas. Each serving is 3/4 of a pizza. How many servings can you get from the 8 pizzas?
We can see that each pizza yields more than one serving (since 3/4 is less than a whole pizza). To calculate the precise number of servings:
-
Servings per pizza: One pizza has four quarters, and you get one serving with three of them (3/4).
-
Total servings: Since each pizza gives you a little more than one serving, and you have 8 pizzas, the total number of servings will be slightly more than 8.
While this method isn't as precise for complex calculations, it provides a valuable visual understanding of what fraction division represents.
Method 3: Converting to a Common Denominator
This method is less common for dividing whole numbers by fractions but demonstrates a strong understanding of fraction manipulation:
-
Convert the whole number to a fraction: We can rewrite 8 as 8/1.
-
Find a common denominator: The common denominator for 1 and 4 is 4. We change 8/1 to an equivalent fraction with a denominator of 4:
(8/1) × (4/4) = 32/4
-
Divide the numerators: Now we divide the numerators:
32/4 ÷ 3/4 = 32 ÷ 3 = 32/3
This again leads us to the improper fraction 32/3, which, as shown before, simplifies to 10 2/3.
Why Understand Different Methods?
Using multiple methods reinforces your understanding of the underlying mathematical principles. Each approach highlights different aspects of fraction division, offering various perspectives on solving the problem. This deeper understanding is crucial for tackling more complex fraction problems and builds confidence in your mathematical abilities.
Real-World Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it's incredibly useful in everyday life. Here are a few examples:
-
Cooking: Recipes often require adjustments based on the number of servings. If a recipe calls for 3/4 cup of flour for 1 serving and you want to make 8 servings, you'll need to divide 8 by 3/4.
-
Construction: Many construction projects involve precise measurements using fractions of inches or feet. Dividing a larger measurement by a smaller fractional one is essential for accurate planning and cutting.
-
Sewing and Fabric: Similar to construction, sewing projects frequently require calculations involving fractions of yards or inches.
-
Finance: Calculating portions of shares, splitting bills, or determining percentages often involves fraction division.
Expanding Your Knowledge: More Complex Fraction Problems
Once you've mastered dividing a whole number by a fraction, you can move on to more challenging problems:
-
Dividing a fraction by a fraction: This involves applying the "Keep, Change, Flip" method consistently. For example, (1/2) ÷ (1/4) would become (1/2) × (4/1) = 2.
-
Dividing mixed numbers: This requires converting mixed numbers into improper fractions before applying the "Keep, Change, Flip" method. For example, to divide 2 1/2 by 1 1/4, first convert to 5/2 and 5/4, and then proceed.
-
Dividing decimals by fractions: Convert the decimals to fractions, then proceed as with dividing fractions by fractions.
Conclusion: Mastering Fraction Division
Understanding how to divide 8 by 3/4, and mastering fraction division in general, is a critical skill with far-reaching applications. By using different methods and exploring real-world examples, you'll build a strong foundation in mathematics and improve your ability to solve problems creatively and efficiently. Remember to practice regularly to reinforce your learning and build confidence in your mathematical abilities. The key takeaway is that regardless of the method used, the answer remains consistent: 10 2/3. This consistent result validates the understanding of the underlying principles and techniques applied. Continue to practice and explore different problem sets to fully grasp the nuances of fraction division.
Latest Posts
Latest Posts
-
How Much Is A Car After Taxes
May 25, 2025
-
4 7 8 As An Improper Fraction
May 25, 2025
-
What Is 20 Percent Of 120000
May 25, 2025
-
Gcf Of 10 15 And 30
May 25, 2025
-
3 4 Divided By 7 12
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 8 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.