3 4 Divided By 7 12
listenit
May 25, 2025 · 4 min read
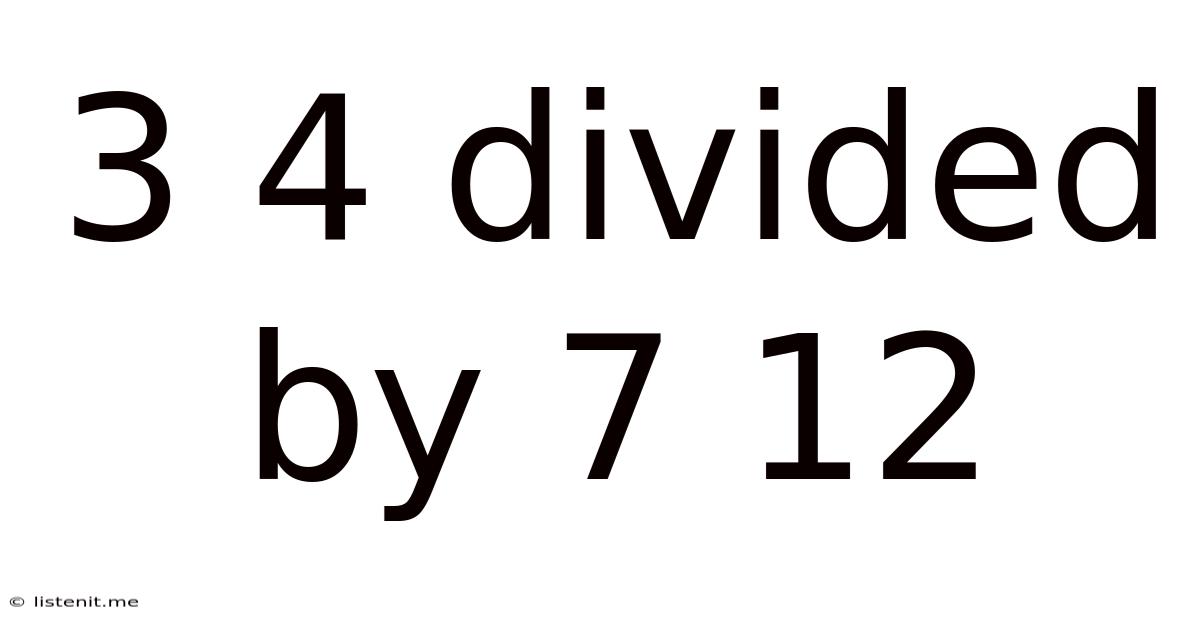
Table of Contents
Deconstructing the Mathematical Phrase: "3 4 divided by 7 12"
The seemingly simple phrase "3 4 divided by 7 12" presents a fascinating challenge in mathematical interpretation. Its ambiguity highlights the crucial role of notation and order of operations in achieving a clear and unambiguous solution. This article will delve into the various ways this phrase can be understood, explore the underlying mathematical principles, and demonstrate how different interpretations lead to vastly different results. We'll also touch on the importance of clear communication in mathematics and how to avoid similar ambiguities in the future.
Understanding the Ambiguity: The Role of Notation
The core problem stems from the lack of explicit operators between the numbers. Is "3 4" meant to represent 34, 3 multiplied by 4 (3 x 4 = 12), 3 added to 4 (3 + 4 = 7), or something else entirely? The same uncertainty applies to "7 12." Without parentheses or explicitly stated operators (+, -, x, ÷), multiple interpretations are possible, leading to different solutions.
This ambiguity emphasizes the critical importance of precise mathematical notation. In formal mathematical expressions, parentheses are essential for specifying the order of operations and removing any potential for misinterpretation. Proper notation is the cornerstone of clear communication in mathematics, ensuring that everyone understands and agrees on the intended calculations.
Potential Interpretations and Their Solutions
Let's explore some plausible interpretations of "3 4 divided by 7 12":
Interpretation 1: (3 x 4) ÷ (7 x 12)
This interpretation assumes that "3 4" means 3 multiplied by 4, and "7 12" means 7 multiplied by 12. Following the order of operations (PEMDAS/BODMAS), we perform the multiplications first:
- (3 x 4) = 12
- (7 x 12) = 84
Then, we perform the division:
- 12 ÷ 84 = 1/7 or approximately 0.1429
Interpretation 2: (3 + 4) ÷ (7 + 12)
Here, we assume that "3 4" represents 3 plus 4, and "7 12" represents 7 plus 12. Again, following the order of operations:
- (3 + 4) = 7
- (7 + 12) = 19
The division is then:
- 7 ÷ 19 = 7/19 or approximately 0.3684
Interpretation 3: 34 ÷ 712
This interpretation treats "3 4" as the number 34 and "7 12" as the number 712. The solution is a simple division:
- 34 ÷ 712 = 17/356 or approximately 0.0477
Interpretation 4: (34) ÷ (712) (Alternative to Interpretation 3)
This interpretation is functionally identical to Interpretation 3. The use of parentheses adds clarity but does not change the result.
Interpretation 5: Other possibilities:
We could also consider interpretations involving subtraction, exponentiation, or a combination of operations, but these are less likely given the lack of suggestive symbols. However, the point remains that without explicit notation, numerous interpretations are plausible.
The Importance of Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), plays a crucial role in determining the correct solution when multiple operations are present. These rules dictate the sequence in which operations should be performed to ensure consistency and avoid ambiguity. In the examples above, we consistently applied the order of operations to arrive at the solutions for each interpretation. Without adhering to these rules, the results would be inconsistent and potentially incorrect.
Implications for Programming and Computer Science
The ambiguity in "3 4 divided by 7 12" directly relates to how programming languages and computer systems handle mathematical expressions. Programming languages require strict adherence to syntax and order of operations. Without proper parentheses and operators, the compiler or interpreter would likely produce an error or a result that differs from the intended calculation. Therefore, understanding the importance of unambiguous mathematical notation is crucial for anyone working in programming or computer science.
The Power of Parentheses: Ensuring Clarity
The most effective way to avoid the ambiguities demonstrated above is to use parentheses to clearly indicate the order of operations. For instance:
- ((3 x 4) ÷ (7 x 12)) = 1/7
- ((3 + 4) ÷ (7 + 12)) = 7/19
- (34 ÷ 712) = 17/356
By using parentheses, there is no room for misinterpretation. The intended calculation is clearly defined, leading to a single, unambiguous answer. This highlights the vital role of parentheses and precise notation in mathematical communication.
Conclusion: Precision in Mathematical Communication
The phrase "3 4 divided by 7 12" serves as a powerful example of the need for precise and unambiguous mathematical notation. The multiple interpretations and resulting different solutions highlight the dangers of relying on implied operations or unclear syntax. The consistent application of order of operations (PEMDAS/BODMAS) and the strategic use of parentheses are crucial for ensuring that mathematical expressions are clearly understood and lead to accurate results. This principle extends beyond simple arithmetic problems; it is fundamental to all areas of mathematics, computer science, and any field requiring precise numerical calculations. By adopting clear and consistent notation, we avoid ambiguity and pave the way for effective communication and collaboration in the mathematical world. In essence, the clarity of mathematical expression is not just a matter of style; it's a matter of accuracy and reliable communication. Always prioritize clear and unambiguous notation to avoid confusion and ensure that your mathematical expressions are correctly understood.
Latest Posts
Latest Posts
-
Age Of Someone Born In 1981
May 25, 2025
-
3 1 8 As An Improper Fraction
May 25, 2025
-
What Is 25 Off 75 Dollars
May 25, 2025
-
What Percent Is Equivalent To 11 20
May 25, 2025
-
What Is 75 Off Of 35
May 25, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 7 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.