What Is 7/25 As A Percent
listenit
Apr 05, 2025 · 4 min read
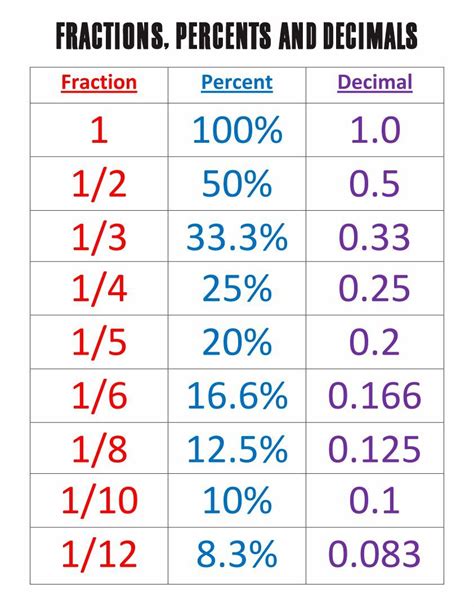
Table of Contents
What is 7/25 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding financial reports and statistical data. This comprehensive guide will delve into the process of converting the fraction 7/25 into a percentage, providing a step-by-step explanation, exploring different methods, and highlighting the practical significance of this conversion. We'll also touch upon related concepts and provide further examples to solidify your understanding.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the concepts of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 7/25, 7 is the numerator and 25 is the denominator.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." Percentages are often denoted by the symbol "%". For instance, 25% means 25 parts out of 100.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is perhaps the most straightforward method. It involves two steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, we simply divide the numerator by the denominator:
7 ÷ 25 = 0.28
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.28 × 100 = 28%
Therefore, 7/25 is equal to 28%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method relies on the principle of equivalent fractions. We aim to find a fraction equivalent to 7/25 that has a denominator of 100. Since percentages are fractions out of 100, this directly gives us the percentage.
To find an equivalent fraction with a denominator of 100, we need to determine what number we must multiply the denominator (25) by to get 100. This is 4 (since 25 × 4 = 100).
Crucially, whatever we multiply the denominator by, we must also multiply the numerator by the same number to maintain the equivalence of the fraction.
Therefore, we multiply both the numerator and the denominator of 7/25 by 4:
(7 × 4) / (25 × 4) = 28/100
Since 28/100 means 28 parts out of 100, this is equivalent to 28%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. We can set up a proportion:
7/25 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
7 × 100 = 25 × x
700 = 25x
Now, divide both sides by 25:
x = 700/25 = 28
Therefore, x = 28, meaning 7/25 is equal to 28%.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages has numerous practical applications in various fields:
-
Finance: Calculating interest rates, discounts, tax rates, and profit margins all involve percentage calculations. Understanding how to convert fractions to percentages is essential for making informed financial decisions.
-
Statistics: Percentages are frequently used to represent data in statistical analyses. Converting fractions to percentages allows for easier interpretation and comparison of data.
-
Science: In scientific experiments and data analysis, percentages are often used to express ratios and proportions.
-
Everyday Life: Calculating tips, discounts in stores, and understanding survey results all involve working with percentages.
Further Examples
Let's practice with a few more examples:
- What is 15/20 as a percentage?
Using Method 1: 15 ÷ 20 = 0.75 => 0.75 × 100 = 75%
Using Method 2: (15 × 5) / (20 × 5) = 75/100 = 75%
- What is 3/8 as a percentage?
Using Method 1: 3 ÷ 8 = 0.375 => 0.375 × 100 = 37.5%
Using Method 2: This one is a bit trickier since 8 doesn't divide evenly into 100. We can use decimals: 3 ÷ 8 = 0.375, then multiply by 100 to get 37.5%.
- What is 1/4 as a percentage?
This one is a common and easily remembered fraction. 1/4 = 0.25, and 0.25 x 100 = 25%. Alternatively, because 1/4 is equivalent to 25/100, we already have the percentage expressed as 25%.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a crucial skill with far-reaching applications. Understanding the different methods—whether it's converting to a decimal first, finding an equivalent fraction with a denominator of 100, or using proportions—will empower you to tackle various percentage-related problems with confidence. The ability to perform these conversions accurately contributes significantly to success in various academic and professional contexts, making it a valuable mathematical tool in your skillset. Remember to practice regularly to enhance your proficiency and improve your understanding of this essential concept.
Latest Posts
Latest Posts
-
How Many Pounds Is A Pint
Apr 05, 2025
-
How Does Outliers Affect The Mean
Apr 05, 2025
-
What Is A Row In The Periodic Table
Apr 05, 2025
-
What Is The Square Root Of 140
Apr 05, 2025
-
How Do You Write 50 As A Decimal
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 7/25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
