What Is 6 Percent Of 20000
listenit
May 25, 2025 · 5 min read
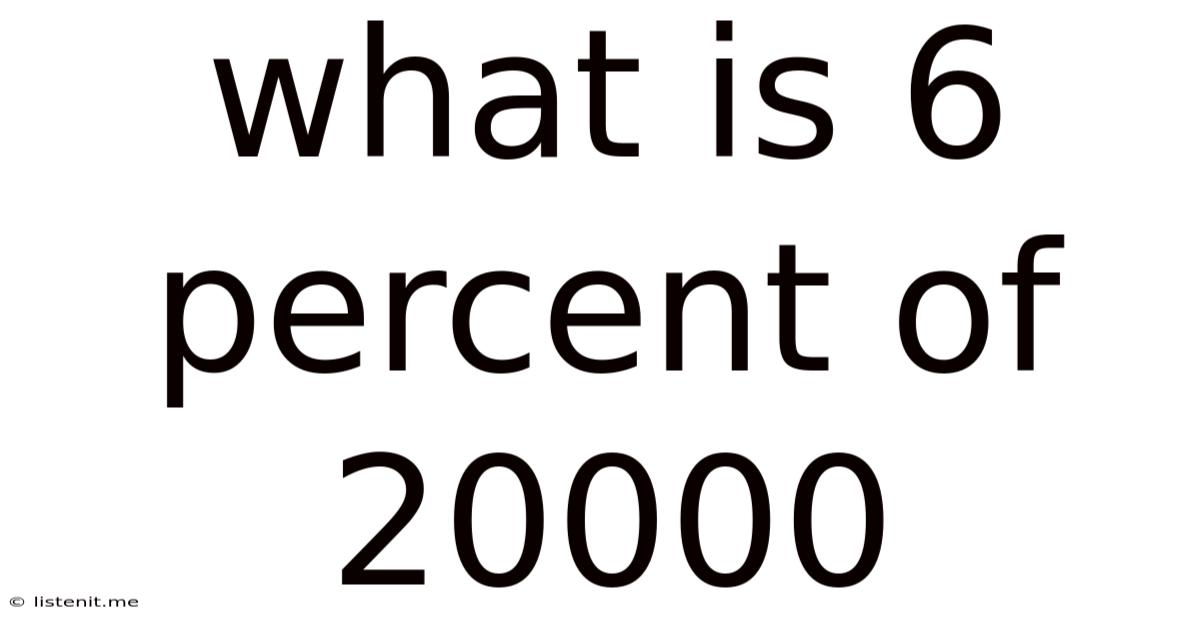
Table of Contents
What is 6 Percent of 20,000? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill in various aspects of life, from financial planning and budgeting to understanding statistics and data analysis. This comprehensive guide will not only answer the question, "What is 6 percent of 20,000?" but also delve into the underlying concepts, providing you with the tools and knowledge to tackle similar percentage problems with confidence.
Understanding Percentages
Before we dive into the calculation, let's establish a clear understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" denotes percentage. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Percentages are used extensively to represent proportions, ratios, and changes in various contexts. Understanding percentages is crucial for making informed decisions in numerous situations.
Calculating 6 Percent of 20,000: The Methods
There are several ways to calculate 6 percent of 20,000. We'll explore the most common and straightforward methods:
Method 1: Using the Decimal Equivalent
This method is perhaps the most efficient and widely used approach. It involves converting the percentage to its decimal equivalent and then multiplying it by the given number.
-
Convert the percentage to a decimal: To convert 6% to a decimal, divide it by 100: 6% ÷ 100 = 0.06
-
Multiply the decimal by the number: Multiply the decimal equivalent (0.06) by 20,000: 0.06 × 20,000 = 1200
Therefore, 6 percent of 20,000 is 1200.
Method 2: Using the Fraction Equivalent
This method involves converting the percentage to a fraction and then multiplying it by the given number.
-
Convert the percentage to a fraction: 6% can be written as 6/100.
-
Simplify the fraction (optional): The fraction 6/100 can be simplified to 3/50.
-
Multiply the fraction by the number: Multiply the simplified fraction (3/50) by 20,000: (3/50) × 20,000 = 3 × (20,000/50) = 3 × 400 = 1200
Again, we arrive at the answer: 6 percent of 20,000 is 1200.
Method 3: Using Proportions
This method is particularly helpful in understanding the relationship between the percentage, the part, and the whole. It involves setting up a proportion and solving for the unknown value.
Let 'x' represent 6 percent of 20,000. We can set up the proportion as follows:
6/100 = x/20,000
To solve for 'x', we can cross-multiply:
100x = 6 × 20,000
100x = 120,000
x = 120,000/100
x = 1200
Once more, the calculation confirms that 6 percent of 20,000 is 1200.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in a wide range of real-world scenarios. Here are some examples:
Finance and Budgeting:
-
Calculating interest: Understanding interest rates is crucial for managing loans, investments, and savings accounts. Calculating the interest earned or paid often involves percentage calculations. For instance, if you have a savings account with a 3% annual interest rate and a balance of $10,000, you can calculate your yearly interest by finding 3% of $10,000.
-
Determining discounts and sales tax: Stores frequently offer discounts as percentages (e.g., 20% off). Calculating the final price after a discount requires percentage calculations. Similarly, sales tax is often expressed as a percentage of the purchase price.
-
Analyzing financial statements: Financial statements, such as income statements and balance sheets, are filled with percentages that represent key financial ratios and metrics. Analyzing these percentages is vital for understanding a company's financial health.
Statistics and Data Analysis:
-
Calculating percentages in surveys and polls: Surveys and polls frequently present data in percentage terms. Understanding how to interpret and analyze these percentages is essential for drawing meaningful conclusions.
-
Representing proportions and distributions: Percentages are used to represent proportions and distributions within datasets. For example, the percentage of a population belonging to a particular demographic group is expressed as a percentage.
-
Understanding statistical significance: In statistical analysis, percentages are often used to express the level of statistical significance of results.
Everyday Life:
-
Calculating tips and gratuities: In many cultures, it's customary to leave a tip or gratuity at restaurants and other service establishments. Tips are often calculated as a percentage of the total bill.
-
Understanding sales and promotions: Understanding percentage discounts and promotional offers is essential for making informed purchasing decisions.
-
Measuring progress towards goals: Tracking progress towards goals, such as saving money or losing weight, often involves calculating percentages to assess how far along you are.
Advanced Percentage Calculations and Problem Solving
While calculating 6% of 20,000 is straightforward, more complex percentage problems might involve finding the percentage increase or decrease, determining the original value given a percentage change, or solving for unknown percentages. Let’s explore some:
Finding Percentage Increase or Decrease:
Suppose a product’s price increased from $100 to $120. To find the percentage increase:
- Find the difference: $120 - $100 = $20
- Divide the difference by the original value: $20 / $100 = 0.2
- Multiply by 100 to express as a percentage: 0.2 * 100 = 20%
Therefore, the price increased by 20%.
Finding the Original Value After a Percentage Change:
If a product is on sale at $80 after a 20% discount, to find the original price:
- Consider the remaining percentage: 100% - 20% = 80%
- Set up an equation: 80% * Original Price = $80
- Solve for the original price: Original Price = $80 / 0.8 = $100
The original price was $100.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The more you practice, the more comfortable and efficient you'll become with percentage calculations.
-
Use a Calculator: For complex calculations, a calculator can save time and ensure accuracy.
-
Understand the Concepts: Focusing on understanding the underlying concepts of percentages will make problem-solving easier.
-
Break Down Complex Problems: Complex percentage problems can often be broken down into smaller, more manageable steps.
-
Check Your Work: Always double-check your calculations to avoid errors.
By understanding the fundamental principles of percentage calculations and practicing various problem-solving techniques, you'll be well-equipped to handle any percentage-related task confidently. Remember, the ability to work with percentages is a valuable skill applicable to numerous aspects of life, both personal and professional. So, whether you're managing your finances, analyzing data, or simply tackling everyday problems, mastering percentages will empower you to make informed decisions and achieve your goals.
Latest Posts
Latest Posts
-
Whats 1 2 Of 2 3
May 26, 2025
-
Find The Area Between Two Z Scores
May 26, 2025
-
30 Out Of 50 Is What Percent
May 26, 2025
-
What Is The Greatest Common Factor Of 14 And 35
May 26, 2025
-
How Many Calories Do I Burn Reading
May 26, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 Percent Of 20000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.