What's 1 2 Of 2 3
listenit
May 26, 2025 · 5 min read
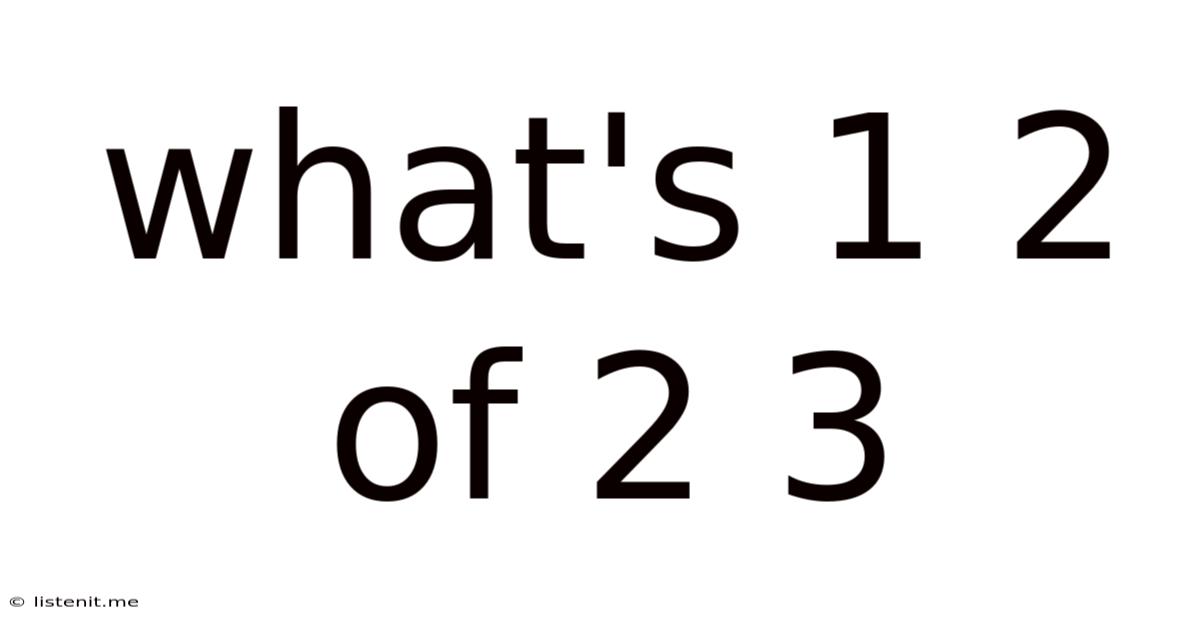
Table of Contents
What's 1/2 of 2/3? A Deep Dive into Fractions and Their Applications
Understanding fractions is fundamental to mathematics and has far-reaching applications in various fields. This article will not only answer the seemingly simple question, "What's 1/2 of 2/3?", but will also delve into the underlying principles of fraction multiplication, offering practical examples and exploring its relevance in real-world scenarios.
Understanding Fractions: A Quick Refresher
Before we tackle the main problem, let's revisit the basics of fractions. A fraction represents a part of a whole. It consists of two numbers:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator is 1 (we have one part), and the denominator is 2 (the whole is divided into two equal parts).
Multiplying Fractions: The Process
Multiplying fractions is a straightforward process:
- Multiply the numerators: Multiply the top numbers together.
- Multiply the denominators: Multiply the bottom numbers together.
- Simplify (if possible): Reduce the resulting fraction to its simplest form by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Solving the Problem: 1/2 of 2/3
Now, let's solve the problem at hand: What's 1/2 of 2/3? "Of" in mathematics usually signifies multiplication. Therefore, we need to multiply 1/2 by 2/3:
(1/2) * (2/3) = (1 * 2) / (2 * 3) = 2/6
This fraction, 2/6, can be simplified. Both the numerator (2) and the denominator (6) are divisible by 2:
2/6 = (2 ÷ 2) / (6 ÷ 2) = 1/3
Therefore, 1/2 of 2/3 is 1/3.
Real-World Applications of Fraction Multiplication
The seemingly simple operation of multiplying fractions has numerous applications in daily life and various professional fields. Here are a few examples:
1. Cooking and Baking: Recipes often require fractional amounts of ingredients. For example, a recipe might call for 1/2 of a 2/3 cup of sugar. Understanding fraction multiplication helps determine the exact amount needed (1/3 cup in this case).
2. Construction and Engineering: Precise measurements are crucial in construction and engineering. Calculations involving fractions are frequently needed to determine the appropriate lengths, areas, and volumes for various components. For example, calculating the area of a wall that's 2 1/2 meters by 3 2/3 meters involves fraction multiplication.
3. Finance and Investments: Fractions are used extensively in finance to represent proportions of ownership, interest rates, and investment returns. Calculating compound interest, for instance, frequently involves working with fractions and their multiplication.
4. Data Analysis and Statistics: Fractions are essential in representing probabilities and proportions in data analysis and statistics. For instance, if 2/5 of a sample group responded positively to a survey, and 1/2 of that positive group showed further interest, fraction multiplication helps determine the overall percentage.
5. Science and Medicine: Many scientific calculations, especially in fields like chemistry and physics, involve fractions. Dosage calculations in medicine often require precise fraction multiplication to ensure accurate medication administration.
6. Sewing and Tailoring: In sewing and tailoring, precise measurements are essential, and frequently involve fractions of inches or centimeters. Calculating fabric requirements for a garment often involves fraction multiplication to account for seams and adjustments.
7. Software Development: While not as immediately obvious, fraction multiplication finds its way into software algorithms. Calculations related to graphics, game development, and simulations may involve fraction-based computations.
8. Time Management: Scheduling and time allocation can benefit from fractional understanding. If a project takes 2/3 of a day to complete and you only have 1/2 of a day available, fraction multiplication helps in assessing the feasibility of the task within the given timeframe.
Beyond the Basics: More Complex Fraction Problems
While the initial problem was straightforward, fraction multiplication can become more complex when dealing with mixed numbers (numbers with a whole number part and a fractional part) or when performing multiple fraction multiplications.
Mixed Numbers: To multiply fractions involving mixed numbers, first convert the mixed numbers into improper fractions (where the numerator is greater than or equal to the denominator). Then, proceed with the standard fraction multiplication steps.
Multiple Multiplications: When multiplying more than two fractions, simply multiply all the numerators together and all the denominators together. Simplify the result to its lowest form.
Mastering Fractions: A Key to Mathematical Proficiency
Proficiency in working with fractions is crucial for success in various mathematical disciplines. Understanding the concepts, processes, and applications of fractions, such as multiplication, provides a solid foundation for tackling more advanced mathematical problems. From everyday tasks to complex scientific calculations, the ability to work comfortably with fractions is an invaluable skill. Regular practice and exposure to diverse problems will significantly improve your understanding and ability in working with fractions.
Improving Your Fraction Skills:
Here are some tips to help you improve your fraction skills:
-
Practice Regularly: The more you practice, the more confident and efficient you'll become. Work through various problems, starting with simpler ones and gradually increasing the difficulty.
-
Visual Aids: Use visual aids such as diagrams, pie charts, or fraction bars to represent fractions and understand their values more clearly. This is particularly helpful for visualizing fraction multiplication.
-
Online Resources: There are many excellent online resources, including interactive exercises and tutorials, that can aid in understanding and practicing fraction operations.
-
Real-World Application: Look for opportunities to apply fraction skills in your daily life. This can make learning more engaging and reinforce your understanding.
-
Seek Help: If you encounter difficulties, don't hesitate to seek assistance from teachers, tutors, or online communities dedicated to math support.
By mastering the concepts and techniques involved in fraction multiplication, you will not only be able to solve problems like "What's 1/2 of 2/3?" with ease, but you will also be equipped with a valuable mathematical skill applicable in a wide range of situations. The ability to confidently manipulate and interpret fractions is a cornerstone of numerical literacy and opens doors to understanding and tackling a diverse range of challenges in various fields.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 3 And 6
May 26, 2025
-
72 Hours From Now Is What Day
May 26, 2025
-
Round 583027 74847 To The Nearest Hundred
May 26, 2025
-
How Many Calories Should A 145 Pound Woman Eat
May 26, 2025
-
How Many Calories To Maintain 130 Pounds Female
May 26, 2025
Related Post
Thank you for visiting our website which covers about What's 1 2 Of 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.