What Is 5 To The 4 Power
listenit
May 23, 2025 · 5 min read
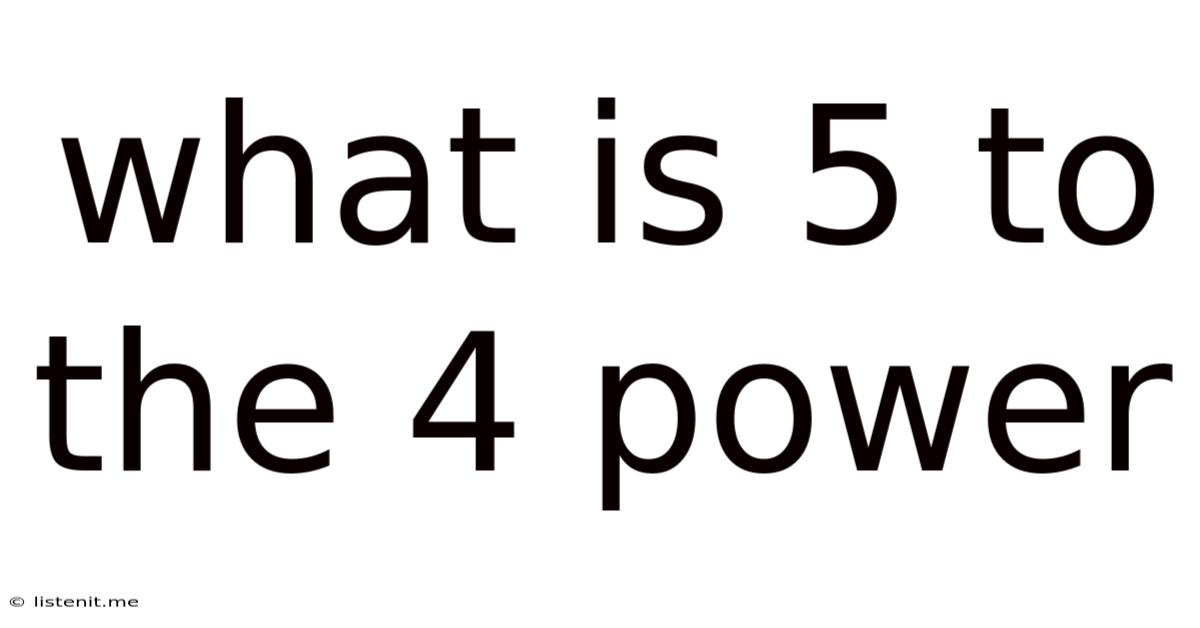
Table of Contents
What is 5 to the 4th Power? A Deep Dive into Exponents and Their Applications
The question, "What is 5 to the 4th power?" might seem simple at first glance. However, understanding this seemingly straightforward calculation opens the door to a broader comprehension of exponents, their properties, and their wide-ranging applications in various fields. This article delves into the meaning of 5 to the power of 4, exploring its calculation, the underlying principles of exponentiation, and showcasing its relevance in diverse contexts.
Understanding Exponents: The Basics
Before we tackle 5 to the 4th power, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. It's represented as a small superscript number to the right of the base. For example, in the expression 5⁴, '5' is the base and '4' is the exponent. This means we multiply 5 by itself four times.
Calculating 5 to the 4th Power
The calculation is straightforward:
5⁴ = 5 x 5 x 5 x 5 = 625
Therefore, 5 to the 4th power is 625.
Expanding the Understanding: Properties of Exponents
The concept of exponentiation extends far beyond this simple calculation. Understanding the properties of exponents is crucial for tackling more complex mathematical problems. Here are some key properties:
-
Product of Powers: When multiplying two numbers with the same base, you add the exponents: aᵐ x aⁿ = aᵐ⁺ⁿ. For example, 5² x 5³ = 5⁵ = 3125.
-
Quotient of Powers: When dividing two numbers with the same base, you subtract the exponents: aᵐ / aⁿ = aᵐ⁻ⁿ (where a ≠ 0). For example, 5⁵ / 5² = 5³ = 125.
-
Power of a Power: When raising a power to another power, you multiply the exponents: (aᵐ)ⁿ = aᵐⁿ. For example, (5²)³ = 5⁶ = 15625.
-
Power of a Product: When raising a product to a power, you raise each factor to that power: (ab)ⁿ = aⁿbⁿ. For example, (5 x 2)² = 5² x 2² = 25 x 4 = 100.
-
Power of a Quotient: When raising a quotient to a power, you raise both the numerator and denominator to that power: (a/b)ⁿ = aⁿ/bⁿ (where b ≠ 0). For example, (5/2)² = 5²/2² = 25/4 = 6.25.
Negative and Fractional Exponents
Exponents aren't limited to positive integers. Negative exponents represent reciprocals: a⁻ⁿ = 1/aⁿ. Fractional exponents involve roots: aᵐ/ⁿ = ⁿ√(aᵐ). For instance:
- 5⁻² = 1/5² = 1/25 = 0.04
- 5¹/² = √5 ≈ 2.236
Understanding these properties allows you to manipulate and solve complex exponential equations efficiently.
Real-World Applications of Exponents
The concept of 5⁴, and exponents in general, isn't confined to theoretical mathematics. They have practical applications across diverse fields:
-
Compound Interest: Exponents are fundamental to calculating compound interest. The formula A = P(1 + r/n)^(nt) uses exponents to determine the future value (A) of an investment based on the principal (P), interest rate (r), number of times interest is compounded per year (n), and the number of years (t). The power (nt) signifies the compounded effect over time.
-
Population Growth: Exponential growth models are used to describe population increases, whether it's human populations, bacterial colonies, or animal populations. The formula often involves an exponential term that reflects the multiplicative nature of growth.
-
Radioactive Decay: Radioactive decay follows an exponential decay model, where the amount of a radioactive substance decreases exponentially over time. The half-life of a substance is often expressed using exponential functions.
-
Computer Science: Exponents play a critical role in computer science, especially in algorithms and data structures. Computational complexity is often expressed using Big O notation, which frequently involves exponential terms to represent the scaling of algorithms with increasing input size. For example, an algorithm with exponential time complexity will become significantly slower as the input grows.
-
Physics: Exponents appear throughout physics, particularly in equations describing motion, energy, and wave phenomena. For example, the intensity of light decreases exponentially with distance from the source.
-
Engineering: Engineers use exponential functions to model various phenomena, including signal decay in electrical circuits, heat transfer, and structural mechanics.
-
Finance: Beyond compound interest, exponents are crucial in financial modeling, particularly in areas like options pricing and risk assessment. Complex financial instruments often rely on exponential functions to capture the dynamics of market fluctuations.
-
Biology: Exponential functions model various biological processes, such as cell division, enzyme kinetics, and the spread of diseases.
Beyond 5⁴: Exploring Higher Powers and Larger Bases
While we focused on 5⁴, the principles extend to any base and exponent. Understanding the properties of exponents allows us to handle calculations involving much larger numbers and more complex exponents with ease. For instance, calculating 10¹⁰ (ten to the power of ten) is a simple application of these principles, resulting in 10,000,000,000. Similarly, calculating 2²⁰ (two to the power of twenty) demonstrates the rapid growth possible with exponents.
Conclusion: The Power of Understanding Exponents
The seemingly simple question, "What is 5 to the 4th power?" serves as a gateway to a vast and fascinating realm of mathematics. Understanding exponents, their properties, and their diverse applications is not only crucial for solving mathematical problems but also for comprehending and modeling real-world phenomena across multiple disciplines. The ability to work with exponents effectively equips you with a valuable toolset for problem-solving and analytical thinking in various fields of study and professional endeavors. From finance and engineering to biology and computer science, the power of exponents is undeniably pervasive. Mastering this fundamental concept unlocks a deeper appreciation for the elegance and practicality of mathematics.
Latest Posts
Latest Posts
-
Least Common Multiple Of 2 3
May 23, 2025
-
What Day Is It In 18 Days
May 23, 2025
-
How Much Is 15 Of 50
May 23, 2025
-
Common Factors Of 30 And 48
May 23, 2025
-
Greatest Common Factor Of 6 And 9
May 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 To The 4 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.