What Is 5 6 Of 20
listenit
May 24, 2025 · 5 min read
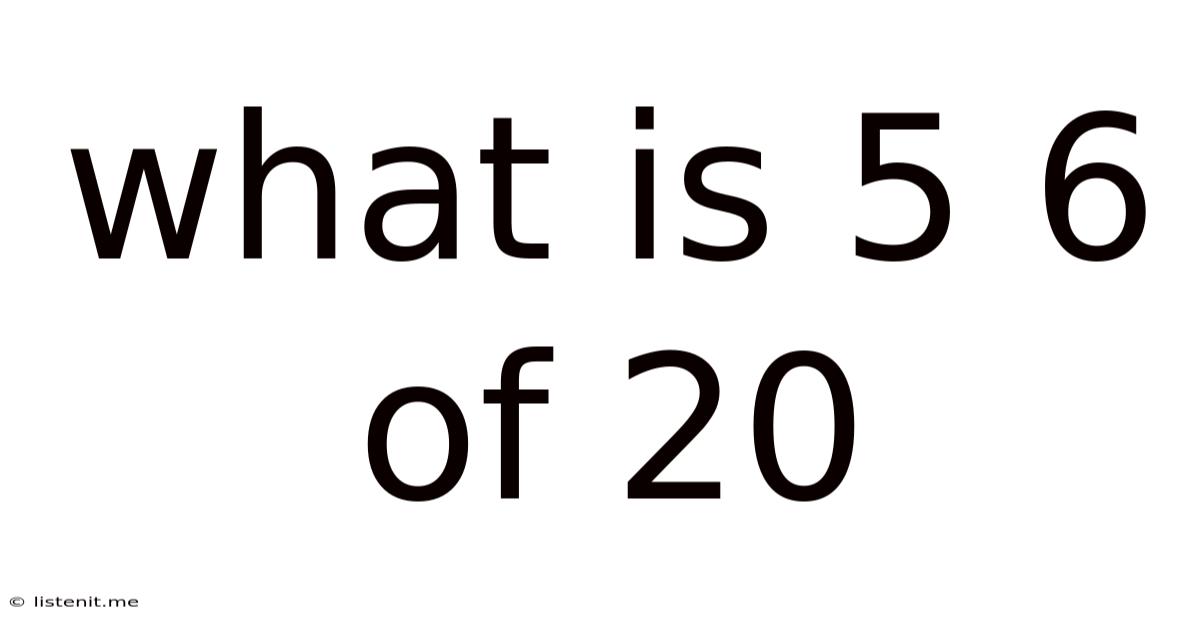
Table of Contents
What is 5/6 of 20? A Comprehensive Guide to Fractions and Their Applications
Understanding fractions is a fundamental skill in mathematics, crucial for various applications in everyday life, from cooking and construction to finance and data analysis. This article delves deep into the question, "What is 5/6 of 20?", providing a step-by-step solution, exploring different methods to solve similar problems, and highlighting the broader context of fractions and their significance.
Understanding the Problem: 5/6 of 20
The phrase "5/6 of 20" represents a fraction of a whole number. It asks us to find what amount constitutes five-sixths of the total number 20. This problem involves a simple multiplication of a fraction with a whole number.
Method 1: Converting the Whole Number into a Fraction
To solve this problem, we can first convert the whole number, 20, into a fraction. Any whole number can be expressed as a fraction by placing it over 1. Therefore, 20 becomes 20/1.
Now our problem becomes: (5/6) * (20/1)
To multiply fractions, we multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together.
(5 * 20) / (6 * 1) = 100/6
This result, 100/6, is an improper fraction (where the numerator is larger than the denominator). To simplify this, we divide the numerator by the denominator:
100 ÷ 6 = 16 with a remainder of 4.
Therefore, 100/6 can be expressed as a mixed number: 16 and 4/6.
We can further simplify the fraction 4/6 by dividing both the numerator and the denominator by their greatest common divisor, which is 2:
4/6 = (4÷2) / (6÷2) = 2/3
So, the final answer is 16 and 2/3. This means 5/6 of 20 is 16 2/3.
Method 2: Simplifying Before Multiplication
Alternatively, we can simplify the fraction before performing the multiplication. Notice that we can simplify 20/6 by dividing both the numerator and the denominator by their greatest common divisor, which is 2:
20/6 = (20÷2) / (6÷2) = 10/3
Now our problem becomes: (5/6) * (10/3)
This simplifies the calculation:
(5 * 10) / (6 * 3) = 50/18
Again, we have an improper fraction. Simplifying by dividing both the numerator and the denominator by their greatest common divisor (2):
50/18 = (50÷2) / (18÷2) = 25/9
Converting this to a mixed number:
25 ÷ 9 = 2 with a remainder of 7
Therefore, 25/9 = 2 and 7/9.
Wait a minute! We got a different answer. Let's investigate. The error lies in a premature simplification step in Method 2, we did not carry out the simplification correctly. Instead of simplifying individually (20/6) before the multiplication, we should continue Method 1 to avoid this error.
This illustrates the importance of following a consistent method and checking your work.
Method 3: Using Decimal Representation
Another approach is to convert the fraction 5/6 into its decimal equivalent:
5 ÷ 6 ≈ 0.8333 (repeating decimal)
Then, multiply this decimal by 20:
0.8333 * 20 ≈ 16.666
This approximates the answer we obtained using the fraction method, confirming that 5/6 of 20 is approximately 16.67.
Real-World Applications of Fractions
Understanding fractions is essential for numerous real-world situations:
1. Cooking and Baking:
Recipes often require fractional amounts of ingredients. For example, a recipe might call for 2/3 cup of sugar or 1/4 teaspoon of salt. Accurate fractional calculations ensure the final product is successful.
2. Construction and Engineering:
Precise measurements are critical in construction and engineering. Fractions are used to determine dimensions, angles, and material quantities. Incorrect fractional calculations can lead to structural problems.
3. Finance:
Fractions are crucial in financial calculations, such as calculating interest rates, discounts, and proportions of investments. Understanding fractions ensures accurate financial management.
4. Data Analysis:
Fractions and percentages are fundamental in data analysis for representing proportions and relationships within datasets. Analysts use fractions to interpret data trends and draw meaningful conclusions.
5. Time Management:
Fractional parts of an hour, like 1/2 hour or 1/4 hour, are commonly used in scheduling and time management.
Expanding on Fraction Concepts
1. Types of Fractions:
- Proper Fractions: The numerator is smaller than the denominator (e.g., 1/2, 3/4).
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 5/4, 7/3).
- Mixed Numbers: A combination of a whole number and a proper fraction (e.g., 2 1/2, 3 3/4).
2. Operations with Fractions:
Beyond multiplication, other operations with fractions include:
- Addition: To add fractions, they must have a common denominator.
- Subtraction: Similar to addition, a common denominator is needed for subtraction.
- Division: To divide fractions, invert the second fraction (reciprocal) and multiply.
3. Converting Fractions to Decimals and Percentages:
Fractions can be converted into decimals by dividing the numerator by the denominator. Decimals can then be converted to percentages by multiplying by 100 and adding a percent sign.
4. Simplifying Fractions:
Simplifying fractions means reducing them to their lowest terms by dividing both the numerator and denominator by their greatest common divisor. This makes fractions easier to work with.
Conclusion: Mastering Fractions for a Better Understanding of the World
The seemingly simple question, "What is 5/6 of 20?", opens a door to a broader understanding of fractions, their various applications, and the importance of precise mathematical calculations. By mastering the concepts and techniques discussed in this article, you'll be equipped to tackle more complex fraction problems and apply your knowledge in diverse real-world scenarios. Remember that careful attention to detail and choosing the right method is key to achieving accurate results. The ability to work with fractions confidently is a valuable asset in various fields, contributing to success in academic pursuits and practical life.
Latest Posts
Latest Posts
-
How Many Calories Are In 1 Point For Weight Watchers
May 25, 2025
-
12 Out Of 50 As A Percentage
May 25, 2025
-
Greatest Common Factor Of 80 And 96
May 25, 2025
-
When Is 20 Hours From Now
May 25, 2025
-
How Many Mph Is 250 Kmh
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 6 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.