What Is 3 4 Minus 1 2
listenit
May 24, 2025 · 5 min read
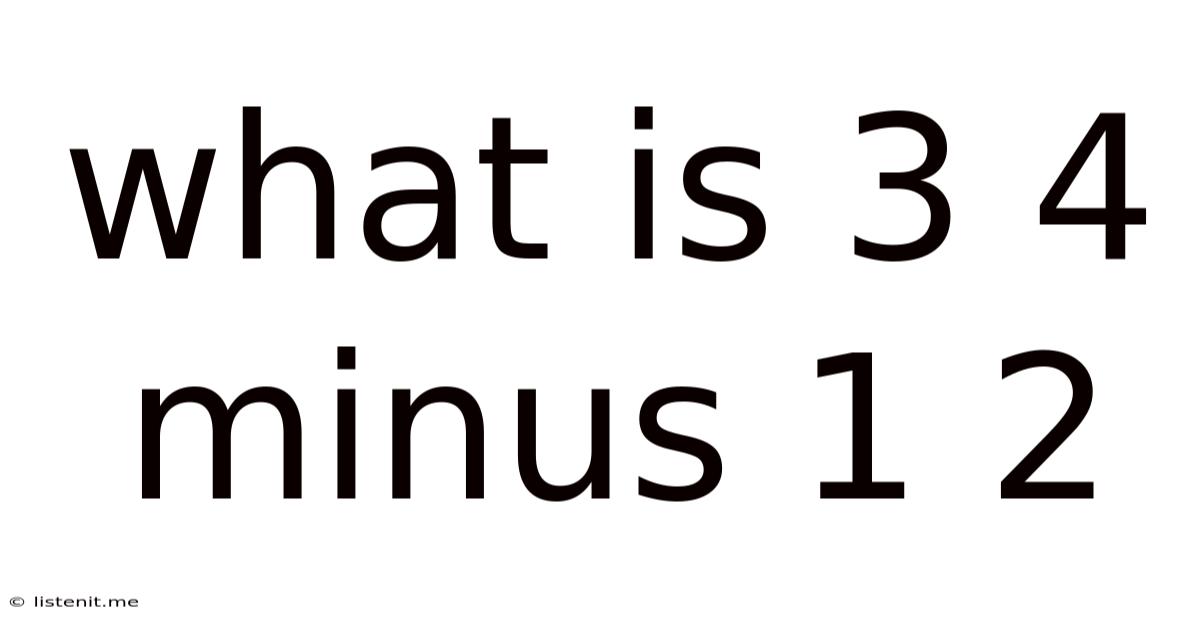
Table of Contents
What is 3/4 Minus 1/2? A Deep Dive into Fraction Subtraction
This seemingly simple question, "What is 3/4 minus 1/2?", opens the door to a deeper understanding of fractions, a fundamental concept in mathematics with far-reaching applications in various fields. This comprehensive guide will not only answer the question but also explore the underlying principles of fraction subtraction, offering multiple approaches and real-world examples to solidify your understanding.
Understanding Fractions: The Building Blocks
Before tackling the subtraction problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator is 3 (we have 3 parts), and the denominator is 4 (the whole is divided into 4 equal parts).
Finding a Common Denominator: The Key to Fraction Subtraction
Subtracting fractions isn't as straightforward as subtracting whole numbers. Before we can subtract, we need a common denominator. This means both fractions must have the same denominator. Why? Because we can only subtract (or add) parts of the same size. Think of it like trying to subtract apples from oranges – you can't do it directly!
Let's look at our problem: 3/4 - 1/2. The denominators are 4 and 2. To find a common denominator, we need to find the least common multiple (LCM) of 4 and 2.
- Multiples of 4: 4, 8, 12, 16...
- Multiples of 2: 2, 4, 6, 8...
The least common multiple is 4. Therefore, we'll convert both fractions to have a denominator of 4.
Converting Fractions to a Common Denominator
To convert 1/2 to an equivalent fraction with a denominator of 4, we need to multiply both the numerator and the denominator by the same number. In this case, we multiply by 2:
(1 * 2) / (2 * 2) = 2/4
Now both fractions have the same denominator:
3/4 - 2/4
Subtracting Fractions with a Common Denominator
Now that we have a common denominator, subtracting is simple. We subtract the numerators and keep the denominator the same:
3/4 - 2/4 = (3 - 2) / 4 = 1/4
Therefore, 3/4 minus 1/2 equals 1/4.
Visualizing Fraction Subtraction: A Pictorial Approach
Visual aids can greatly enhance understanding, especially with fractions. Let's visualize the subtraction:
Imagine a pizza cut into four equal slices. You have three slices (3/4 of the pizza). If you give away two slices (which is equivalent to 1/2 of the pizza), you're left with one slice (1/4 of the pizza).
This visual representation reinforces the result we obtained through calculation.
Alternative Methods for Fraction Subtraction
While the common denominator method is the most common and widely applicable, other methods can be used, particularly for more complex problems. These methods may involve simplifying fractions before performing subtraction.
Method 1: Simplifying Fractions Before Subtraction
Sometimes, simplifying fractions before finding a common denominator can make the calculation easier. However, this is not always the most efficient approach.
Method 2: Using Decimal Equivalents
Fractions can be converted into decimals for subtraction. In our case:
3/4 = 0.75 1/2 = 0.5
0.75 - 0.5 = 0.25
Converting 0.25 back to a fraction gives us 1/4.
This method is useful when dealing with fractions that easily convert to simple decimals, however, it’s not always practical, especially when dealing with fractions that result in repeating or non-terminating decimals.
Real-World Applications of Fraction Subtraction
Fraction subtraction isn't just a mathematical exercise; it has numerous practical applications in everyday life:
-
Cooking and Baking: Recipes often require fractional measurements. Subtracting fractions helps determine the remaining ingredients. For example, if a recipe calls for 3/4 cup of flour and you've already used 1/2 cup, you'll need to calculate how much flour remains.
-
Construction and Measurement: In construction, accurate measurements are crucial. Subtracting fractions is essential for calculating remaining lengths of materials, adjusting dimensions and ensuring precise fit.
-
Finance and Budgeting: Managing finances often involves dealing with fractions of money. Subtracting fractions helps calculate remaining balances, compare expenses and track budgets effectively.
-
Time Management: We often represent time as fractions of an hour or a day. Subtracting fractions helps calculate time spent on tasks or determine time remaining for scheduled events.
Advanced Fraction Subtraction: Tackling More Complex Problems
The principles discussed above extend to more complex fraction subtraction problems involving multiple fractions, mixed numbers (numbers with a whole number and a fraction), and even more challenging scenarios.
Subtracting Mixed Numbers: When subtracting mixed numbers, you may need to borrow from the whole number part. For example, subtracting 2 1/4 from 3 1/2. This requires converting the mixed numbers into improper fractions and then applying the same common denominator approach.
Subtracting Fractions with Unlike Denominators: As the complexity increases, finding the least common denominator becomes crucial for accurate results. Remember, the key is always converting the fractions to have a common denominator.
Conclusion: Mastering Fraction Subtraction
Mastering fraction subtraction is a fundamental skill with wide-ranging applications. By understanding the principles of finding common denominators, visualizing fractions, and employing different approaches, you can confidently tackle various fraction subtraction problems, both simple and complex. The ability to work with fractions efficiently and accurately significantly enhances problem-solving capabilities in various fields and everyday life. Continue practicing, explore different methods and remember the core concepts to solidify your understanding. The ability to work confidently with fractions will serve as a strong foundation for further mathematical explorations.
Latest Posts
Latest Posts
-
What Is 10 To 1 Ratio
May 24, 2025
-
How To Calculate The Mpg Of A Car
May 24, 2025
-
How To Find Dimensions Of Triangle
May 24, 2025
-
If Your 20 What Year Were You Born
May 24, 2025
-
12 Divided By 5 As A Fraction
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 4 Minus 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.