12 Divided By 5 As A Fraction
listenit
May 24, 2025 · 5 min read
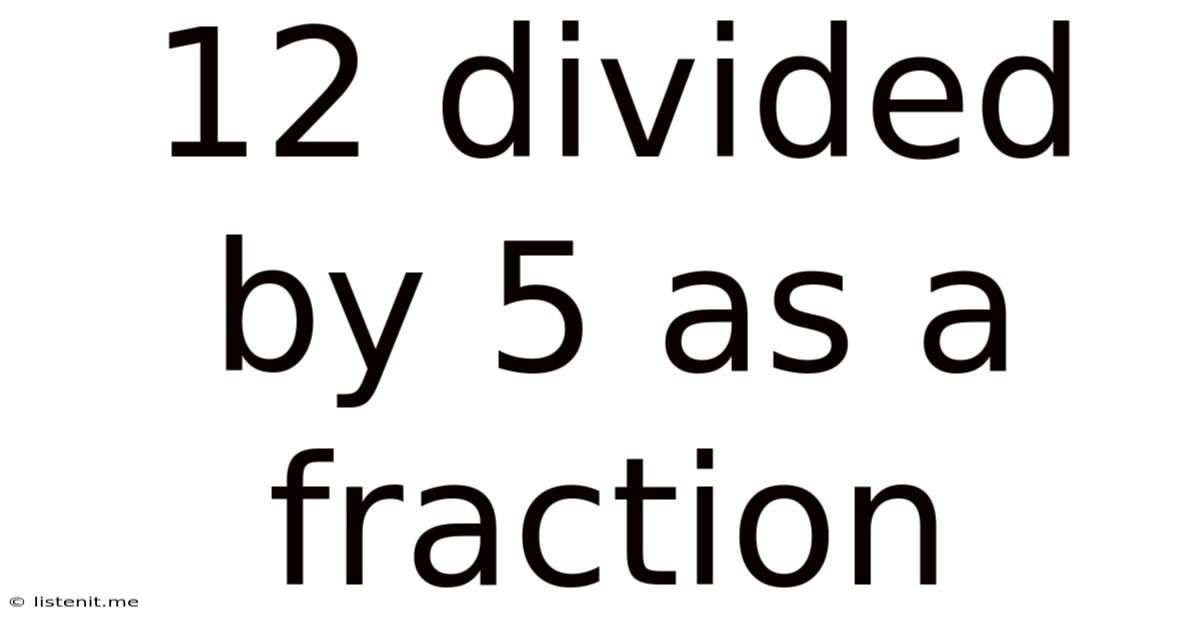
Table of Contents
12 Divided by 5 as a Fraction: A Comprehensive Guide
Dividing numbers is a fundamental arithmetic operation, and expressing the result as a fraction offers valuable insights into the relationship between the dividend and the divisor. This comprehensive guide delves into the process of calculating 12 divided by 5 as a fraction, exploring various methods and applications. We'll cover the basics, explore different representations, and even touch upon the practical uses of understanding this seemingly simple calculation.
Understanding Division and Fractions
Before we dive into the specifics of 12 divided by 5, let's briefly review the concepts of division and fractions. Division is essentially the process of splitting a quantity into equal parts. For instance, dividing 12 cookies among 5 friends means determining how many cookies each friend receives.
A fraction, on the other hand, represents a part of a whole. It's composed of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts the whole is divided into.
Calculating 12 Divided by 5
To express 12 divided by 5 as a fraction, we simply write the dividend (12) as the numerator and the divisor (5) as the denominator:
12/5
This fraction represents the result of dividing 12 into 5 equal parts. However, this is an improper fraction because the numerator (12) is larger than the denominator (5). Improper fractions are perfectly valid, but they're often converted into mixed numbers for easier understanding and practical application.
Converting the Improper Fraction to a Mixed Number
An improper fraction can be converted into a mixed number, which combines a whole number and a proper fraction. To do this, we perform the division:
12 ÷ 5 = 2 with a remainder of 2
The quotient (2) becomes the whole number part of the mixed number. The remainder (2) becomes the numerator of the proper fraction, and the divisor (5) remains the denominator. Therefore, 12/5 as a mixed number is:
2 2/5
This means that when you divide 12 into 5 equal parts, you get 2 whole parts and 2/5 of another part.
Visualizing the Fraction
Visualizing fractions helps solidify understanding. Imagine a pizza cut into 5 equal slices. If you have 12 slices in total (more than one pizza!), you have 2 whole pizzas (10 slices) and 2 slices remaining from a third pizza. This visually represents the 2 2/5.
Decimal Representation
While the fraction and mixed number representations are precise, it's also useful to understand the decimal equivalent. To find the decimal representation of 12/5, simply perform the division:
12 ÷ 5 = 2.4
This decimal, 2.4, is equivalent to both 12/5 and 2 2/5. Different contexts might favor one representation over the others. For instance, fractions are often preferred in precise measurements or when dealing with discrete quantities, while decimals are more common in calculations involving continuous quantities or monetary values.
Applications of 12/5 and its Representations
The seemingly simple calculation of 12 divided by 5 has a surprising number of applications across various fields:
1. Everyday Calculations:
Imagine sharing 12 candies among 5 friends. The fraction 12/5 (or 2 2/5) clearly shows that each friend gets 2 candies, and there are 2 candies left over.
2. Measurement and Engineering:
In engineering and construction, precise measurements are crucial. Representing measurements as fractions allows for greater accuracy than using decimals in certain situations.
3. Finance and Accounting:
Calculations involving shares, percentages, or fractional ownership frequently utilize fractions. Understanding fractions is crucial for handling financial data accurately.
4. Cooking and Baking:
Recipes often require fractional measurements of ingredients. Understanding fractions is crucial for precise baking and cooking.
5. Data Analysis and Statistics:
Fractions are fundamental in representing proportions and probabilities in statistical analysis. Understanding how to manipulate and interpret fractions is key to understanding data.
Equivalent Fractions
It's important to note that 12/5 is not the only way to represent the result of 12 divided by 5 as a fraction. Any fraction that simplifies to 12/5 is equivalent. For example, multiplying both the numerator and denominator by the same number (other than zero) will create an equivalent fraction:
- 24/10
- 36/15
- 48/20
All these fractions simplify to 12/5, demonstrating the flexibility of fractional representation.
Simplifying Fractions
While equivalent fractions exist, it's generally preferred to express fractions in their simplest form. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and the denominator is 1. In the case of 12/5, the GCD of 12 and 5 is 1, meaning the fraction is already in its simplest form.
Further Exploration: Working with Fractions
Understanding 12 divided by 5 as a fraction is a stepping stone to more complex fractional operations. This includes:
- Addition and subtraction of fractions: Requires finding a common denominator.
- Multiplication of fractions: Simply multiply the numerators and the denominators.
- Division of fractions: Invert the second fraction and multiply.
These operations build upon the foundational understanding of fractions and their representations, making them essential skills in mathematics and numerous other fields.
Conclusion: The Significance of Understanding Fractions
The seemingly simple calculation of 12 divided by 5 as a fraction opens the door to a deeper understanding of mathematical concepts and their practical applications. Mastering fractional representations—whether as improper fractions, mixed numbers, or decimals—is crucial for various aspects of life, from everyday tasks to specialized fields. By understanding the different ways to represent and manipulate fractions, you equip yourself with a valuable tool for problem-solving and critical thinking. Remember, the core concept is understanding the relationship between parts and wholes, a principle that extends far beyond simple arithmetic. Continuous practice and exploration of different fractional scenarios will solidify your understanding and improve your overall mathematical proficiency.
Latest Posts
Latest Posts
-
How Much Is 55000 A Year
May 24, 2025
-
3 4 To The Power Of 4
May 24, 2025
-
11 Out Of 40 Is What Percent
May 24, 2025
-
An Annuity Has Accumulated The Cash Value Of 70000
May 24, 2025
-
What Is The Gcf Of 25 And 60
May 24, 2025
Related Post
Thank you for visiting our website which covers about 12 Divided By 5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.