What Is 3/20 As A Percentage
listenit
Apr 02, 2025 · 4 min read
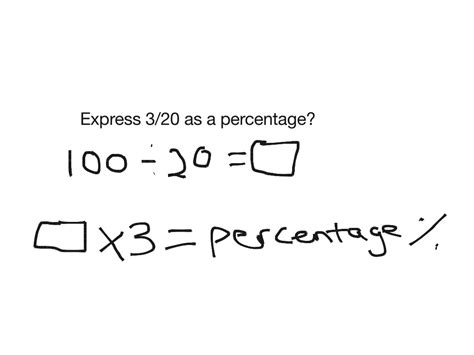
Table of Contents
What is 3/20 as a Percentage? A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding statistics and financial data. This comprehensive guide will delve into the process of converting the fraction 3/20 into a percentage, explaining the method step-by-step and providing additional context and examples to solidify your understanding. We'll also explore the broader concept of fraction-to-percentage conversion and its significance.
Understanding Fractions and Percentages
Before we dive into the conversion, let's briefly review the concepts of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts the whole is divided into. For instance, in the fraction 3/20, 3 is the numerator and 20 is the denominator. This means we have 3 parts out of a total of 20 parts.
Percentages: A percentage represents a fraction out of 100. The symbol "%" signifies "per hundred". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2. Percentages are widely used because they provide a standardized way to compare proportions.
Converting 3/20 to a Percentage: The Step-by-Step Method
There are two primary methods for converting a fraction to a percentage:
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
This method involves two steps:
-
Convert the fraction to a decimal: To do this, divide the numerator by the denominator. In our case:
3 ÷ 20 = 0.15
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%).
0.15 x 100 = 15%
Therefore, 3/20 is equal to 15%.
Method 2: Direct Conversion using Proportion
This method utilizes the concept of proportion. Since a percentage is a fraction out of 100, we can set up a proportion:
3/20 = x/100
To solve for 'x' (the percentage), we can cross-multiply:
20x = 300
x = 300 ÷ 20
x = 15
Therefore, 3/20 is equal to 15%.
Real-World Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages is crucial in various real-world scenarios:
-
Calculating Discounts: If a store offers a 3/20 discount on an item, you can easily convert this fraction to 15% to determine the exact discount amount.
-
Analyzing Financial Data: Understanding financial reports often requires converting fractions representing ratios (e.g., profit margins, debt-to-equity ratios) into percentages for easier comprehension and comparison.
-
Understanding Statistics: Many statistical analyses involve working with fractions and proportions, which are often expressed as percentages for clarity and interpretation. For example, if 3 out of 20 students passed an exam, this can be represented as 15% passing rate.
-
Calculating Test Scores: If you answer 3 out of 20 questions correctly on a test, your score is 15%.
-
Estimating Proportions: Quickly estimating proportions is often easier using percentages. If you see 3 cars out of 20 are red, you can quickly say approximately 15% of the cars are red.
-
Baking and Cooking: Many recipes involve fractional measurements that can be easily converted to percentages for scaling up or down.
Beyond 3/20: Mastering Fraction-to-Percentage Conversions
While we've focused on 3/20, the methods outlined above apply to any fraction. Let's explore a few more examples:
Example 1: Converting 1/4 to a percentage
- Decimal conversion: 1 ÷ 4 = 0.25
- Percentage conversion: 0.25 x 100 = 25%
Therefore, 1/4 is equal to 25%.
Example 2: Converting 7/8 to a percentage
- Decimal conversion: 7 ÷ 8 = 0.875
- Percentage conversion: 0.875 x 100 = 87.5%
Therefore, 7/8 is equal to 87.5%.
Example 3: Converting a more complex fraction like 17/35 to a percentage.
- Decimal Conversion: 17 ÷ 35 ≈ 0.4857
- Percentage Conversion: 0.4857 x 100 ≈ 48.57%
Therefore, 17/35 is approximately 48.57%. Note that we use "approximately" because the decimal representation is a non-terminating decimal.
Tips and Tricks for Efficient Conversion
-
Memorize common fractions and their percentage equivalents: Familiarizing yourself with common fractions like 1/2 (50%), 1/4 (25%), 3/4 (75%), and 1/10 (10%) will greatly speed up your calculations.
-
Use a calculator: For more complex fractions, a calculator can significantly simplify the process. Many calculators have a percentage function that directly converts fractions to percentages.
-
Practice regularly: The more you practice converting fractions to percentages, the more comfortable and proficient you'll become.
Conclusion: The Importance of Understanding Percentages
The ability to convert fractions to percentages is a valuable skill with widespread practical applications. Mastering this skill allows you to confidently tackle various mathematical problems encountered in daily life, academic settings, and professional environments. By understanding the underlying principles and practicing regularly, you can develop a strong understanding of this fundamental concept. Remember, the key is to consistently apply the methods, and with practice, the process will become second nature.
Latest Posts
Latest Posts
-
Write The Sum In Expanded Form
Apr 03, 2025
-
What Is The Shape Of The Orbits Of The Planets
Apr 03, 2025
-
1 1 2 Tablespoons Divided By 2
Apr 03, 2025
-
Lowest Common Multiple Of 25 And 35
Apr 03, 2025
-
Is Square Root Of 16 A Rational Number
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
