What Is 2 Radical 3 Squared
listenit
May 09, 2025 · 5 min read
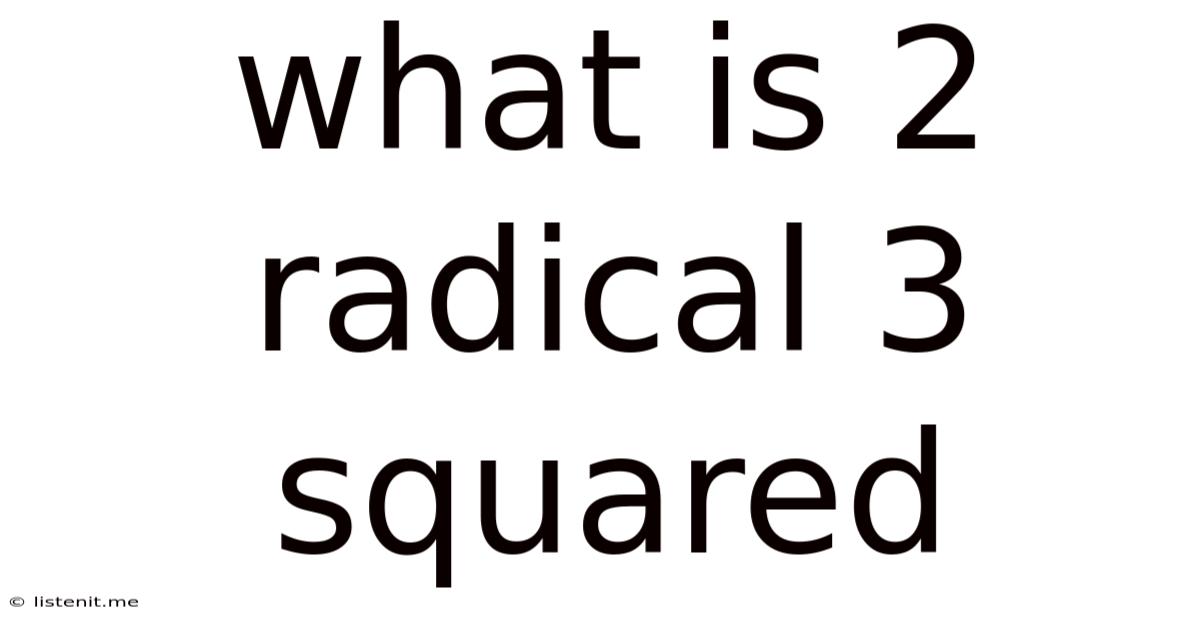
Table of Contents
What is 2√3 Squared? A Deep Dive into Square Roots and Simplification
Understanding the concept of squaring a radical, specifically 2√3 squared, is fundamental in algebra and mathematics in general. This seemingly simple expression opens doors to a broader understanding of mathematical operations, simplification techniques, and the properties of square roots. Let's delve into the intricacies of this calculation, exploring its solution and the underlying principles.
Understanding Square Roots
Before tackling the problem, let's refresh our understanding of square roots. A square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 (√9) is 3, because 3 x 3 = 9. Square roots can be represented with the radical symbol (√) or as exponents with a fractional power (e.g., 9<sup>1/2</sup>).
It's crucial to remember that for positive numbers, there are two square roots: a positive and a negative. However, conventionally, when we talk about the square root of a number, we refer to the principal square root, which is the positive one.
Squaring a Square Root: The Core Concept
Squaring a number means multiplying the number by itself. When we square a square root, we essentially reverse the square root operation. This is because squaring and taking the square root are inverse operations.
Consider the general case: (√a)² = a, where 'a' is a non-negative number. Squaring the square root cancels out the radical, leaving us with the number inside the radical.
Solving 2√3 Squared
Now, let's apply this understanding to the specific problem: (2√3)².
Step 1: Expand the Expression
Following the rules of exponents, we can rewrite the expression as: (2√3)² = 2² x (√3)²
Step 2: Simplify the Terms
- 2² = 2 x 2 = 4
- (√3)² = 3 (as explained above, squaring a square root cancels the radical)
Step 3: Combine the Simplified Terms
Substituting the simplified terms back into the equation, we get: 4 x 3 = 12
Therefore, (2√3)² = 12
Beyond the Calculation: Exploring Related Concepts
Understanding this basic calculation opens doors to exploring more complex mathematical concepts. Let's explore some related ideas:
1. Working with Radicals and Exponents
This problem elegantly demonstrates the interplay between radicals and exponents. The ability to express square roots as fractional exponents (e.g., √3 = 3<sup>1/2</sup>) is crucial in more advanced algebraic manipulations. For example, we could rewrite (2√3)² as (2 * 3<sup>1/2</sup>)² and then apply the power rule (a*b)<sup>n</sup> = a<sup>n</sup> * b<sup>n</sup> to reach the same solution.
2. Simplifying Radical Expressions
Often, we encounter radical expressions that can be simplified. This problem provides a foundation for simplifying more complex radicals. Consider an expression like √75. We can simplify it by factoring 75 into 25 x 3. Then, √75 = √(25 x 3) = √25 x √3 = 5√3. Understanding how squaring radicals works is essential for these simplification processes.
3. Solving Quadratic Equations
The concept of squaring square roots is fundamental in solving quadratic equations. Quadratic equations often involve terms with square roots. The process of isolating the variable often necessitates squaring both sides of the equation, a technique directly related to our problem.
4. Geometry and Pythagorean Theorem
The Pythagorean theorem (a² + b² = c²), which relates the sides of a right-angled triangle, frequently involves square roots. Understanding how to square expressions with radicals is essential for applying and manipulating the theorem effectively in geometric problem-solving.
5. Calculus and Advanced Mathematics
Square roots and their manipulation are pervasive in calculus and higher-level mathematics. Concepts like derivatives and integrals often involve working with functions that contain square roots. A strong foundational understanding of manipulating radicals, as showcased in this problem, forms the bedrock for success in these more advanced areas.
Practical Applications in Real-World Scenarios
While this might seem like a purely abstract mathematical problem, the principles involved have numerous practical applications:
-
Engineering: Calculations related to structures, distances, and forces frequently involve square roots and the Pythagorean theorem. Understanding how to manipulate these expressions is vital for ensuring accurate calculations in engineering designs.
-
Physics: Many physical phenomena, from projectile motion to wave behavior, are described using equations that include square roots. The ability to efficiently solve expressions with radicals is essential for applying and understanding these physical models.
-
Computer Science: Numerical algorithms and computer graphics rely on efficient manipulation of mathematical expressions, including those containing square roots. Understanding these fundamentals is critical for developing optimized software and simulations.
-
Finance: Financial models often use mathematical functions, including square roots, for calculations relating to investments, risk management, and portfolio optimization.
Common Mistakes to Avoid
While the problem itself is relatively straightforward, there are some common mistakes students might make:
-
Incorrect application of the distributive property: Remember that (a + b)² ≠ a² + b². The correct expansion is (a + b)² = a² + 2ab + b². This is a frequent error when dealing with expressions containing sums within parentheses.
-
Incorrect handling of negative numbers: When working with square roots, it's crucial to remember the rules for negative numbers. For example, √(-9) is not -3, it's an imaginary number.
-
Forgetting the order of operations: Always adhere to the order of operations (PEMDAS/BODMAS) to ensure accuracy in calculations involving multiple operations.
Conclusion: Mastering the Fundamentals
Understanding how to square an expression like 2√3 is not just about arriving at the correct numerical answer (12). It's about grasping the fundamental principles of square roots, exponents, and radical simplification. This knowledge forms the groundwork for tackling more complex mathematical problems in various fields. By mastering these seemingly simple concepts, you build a solid foundation for success in higher-level mathematics and its practical applications. Consistent practice and a clear understanding of the underlying principles are key to mastering these essential mathematical skills. Remember, the journey of understanding mathematics is a continuous process of building upon fundamental concepts.
Latest Posts
Latest Posts
-
Cellular Respiration Uses 1 Molecule Of Glucose To Produce Approximately
May 09, 2025
-
How Many Osmoles Are In A Solution Of 1m Naoh
May 09, 2025
-
What Is Difference Between Speed And Acceleration
May 09, 2025
-
Draw The Electron Configuration For A Neutral Atom Of Manganese
May 09, 2025
-
What Are The Three Main Stages Of The Cell Cycle
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 Radical 3 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.