What Is 2 3 Times 1 3
listenit
May 24, 2025 · 5 min read
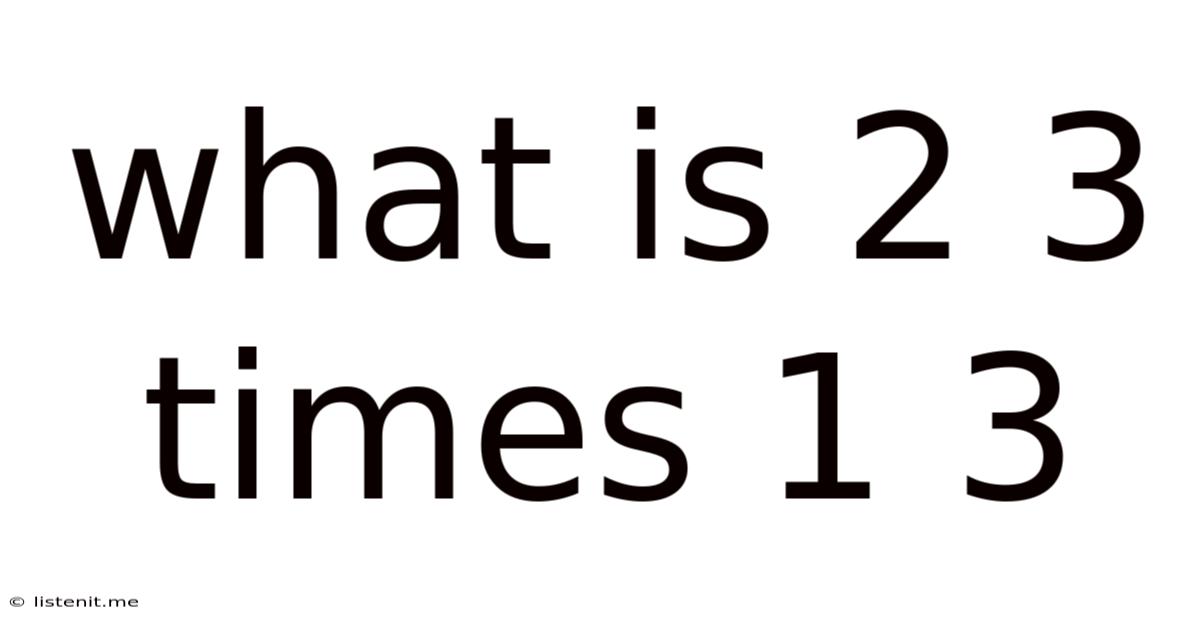
Table of Contents
What is 2/3 Times 1/3? A Deep Dive into Fraction Multiplication
The seemingly simple question, "What is 2/3 times 1/3?" opens a door to a world of fundamental mathematical concepts. While the answer itself is straightforward, understanding the why behind the calculation is crucial for mastering fractions and building a solid foundation in mathematics. This article will not only provide the solution but will explore the underlying principles, offer various approaches to solving the problem, and delve into the broader implications of fraction multiplication.
Understanding Fractions: The Building Blocks
Before tackling the multiplication, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our problem, 2/3 represents two parts out of a total of three equal parts, while 1/3 represents one part out of three. Visualizing these fractions can be incredibly helpful. Imagine a pizza cut into three equal slices. 2/3 would be two slices, and 1/3 would be one slice.
Multiplying Fractions: The Process
Multiplying fractions is a relatively straightforward operation. The process involves two simple steps:
- Multiply the numerators: Multiply the top numbers together.
- Multiply the denominators: Multiply the bottom numbers together.
Let's apply this to our problem:
2/3 * 1/3 = (2 * 1) / (3 * 3) = 2/9
Therefore, 2/3 times 1/3 equals 2/9.
Visualizing the Multiplication
Visualizing the multiplication can enhance understanding. Imagine we have a rectangle representing the whole. Divide this rectangle into three equal columns to represent the denominator of 2/3. Now, shade two of these columns to represent the numerator, 2.
Next, divide the same rectangle into three equal rows to represent the denominator of 1/3. Now, focus only on the area where the shaded columns (2/3) and the rows (1/3) overlap. This overlapping area represents the product of 2/3 and 1/3. You'll find that this overlapping area represents 2 out of 9 equal parts of the whole rectangle – confirming our answer of 2/9.
Different Approaches to Solving the Problem
While the standard method is straightforward, there are other ways to approach this problem that build a deeper understanding of fraction manipulation:
-
Using Decimal Equivalents: We can convert the fractions to decimals before multiplying. 2/3 is approximately 0.667 and 1/3 is approximately 0.333. Multiplying these gives approximately 0.222, which is close to the decimal equivalent of 2/9 (approximately 0.222). This approach, however, introduces rounding errors and isn't as precise as the direct multiplication of fractions.
-
Repeated Addition: Multiplication can be viewed as repeated addition. 2/3 times 1/3 can be interpreted as adding 1/3 to itself two times: 1/3 + 1/3 = 2/3. This is helpful for a conceptual understanding, but it's less efficient for more complex fraction multiplication problems.
Expanding the Concept: Applications of Fraction Multiplication
The ability to multiply fractions is fundamental in various mathematical contexts and real-world applications:
-
Baking and Cooking: Recipes often require fractional measurements. Multiplying fractions is crucial when scaling recipes up or down. For example, if a recipe calls for 1/2 cup of flour, and you want to double the recipe, you'd multiply 1/2 by 2, resulting in 1 cup.
-
Geometry and Area Calculations: Finding the area of a rectangle involves multiplying its length and width. If the length and width are expressed as fractions, you'll need to multiply fractions to find the area.
-
Probability: Probability often involves calculating the likelihood of multiple events occurring. These calculations often involve multiplying fractions representing individual probabilities.
-
Algebra: Fraction multiplication is a building block for more advanced algebraic manipulations, including solving equations and working with polynomials.
Further Exploration: Simplifying Fractions
After multiplying fractions, it's often necessary to simplify the resulting fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD.
In our example, 2/9 is already in its simplest form because 2 and 9 have no common divisors other than 1. However, if we had obtained a fraction like 6/12, we would simplify it to 1/2 by dividing both the numerator and denominator by their GCD, which is 6.
Mastering Fractions: Practice and Resources
The key to mastering fraction multiplication (and fractions in general) lies in consistent practice. Start with simple problems and gradually increase the complexity. There are numerous online resources, worksheets, and textbooks available to assist in your practice.
Remember that understanding the underlying concepts is just as important as memorizing the process. Visualizing the fractions, exploring different approaches, and understanding the real-world applications will solidify your understanding and make you more confident in your mathematical abilities.
Conclusion: Beyond the Simple Calculation
The simple problem of multiplying 2/3 and 1/3 serves as a gateway to a broader understanding of fractions and their significance in mathematics and everyday life. By understanding the process, visualizing the concept, and exploring different approaches, you'll not only be able to solve this specific problem but also build a solid foundation for tackling more complex mathematical challenges. The seemingly simple answer, 2/9, represents a much deeper understanding of the fundamental principles of fraction arithmetic. The journey of understanding fractions is a continuous one, but with practice and a focus on understanding the underlying concepts, anyone can master this essential mathematical tool.
Latest Posts
Latest Posts
-
5am To 12am Is How Many Hours
May 24, 2025
-
What Is 2 1 As A Fraction
May 24, 2025
-
What Is 4 Divided By 1 2
May 24, 2025
-
Cash On Cash Return Calculator Real Estate
May 24, 2025
-
If You Was Born In 1968 How Old Are You
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Times 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.